Т е о р е м а. В ЕП(УП) координаты 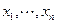 вектора
вектора 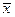 в ОНБ
в ОНБ 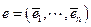 вычисляются по правилу
вычисляются по правилу
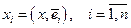 . (3.6)
. (3.6)
Доказательство. Умножим вектор 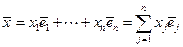 скалярно на
скалярно на 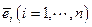 :
:
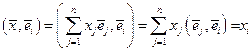 .
.
Таким образом, координаты произвольного элемента относительно ОНБ равны скалярным произведениям этого элемента на соответствующие базисные элементы (проекция элемента 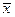 на элемент
на элемент 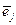 . #
. #
Т е о р е м а. В ЕП(УП) скалярное произведение векторов 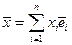 и
и 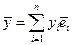 , заданных своими координатами в ОНБ e вычисляется по правилу
, заданных своими координатами в ОНБ e вычисляется по правилу
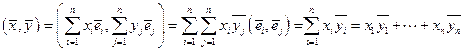 . # (3.7)
. # (3.7)
Замечание. В ЕП черта может быть опущена:
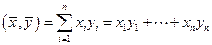
Таким образом, в ОНБ СП любых двух элементов равно сумме произведений соответствующих координат этих элементов.
О п р е д е л е н и е. Матрица 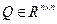 называется ортогональной, если
называется ортогональной, если 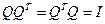 .
.
О п р е д е л е н и е. Матрица 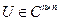 называется унитарной, если
называется унитарной, если 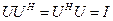 .
.
Т е о р е м а. Во всяком n-мерном ЕП(УП) существует ОНБ.
Д о к а з а т е л ь с т в о. Пусть 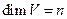 ,
, 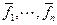 - произвольный базис Е (U). Докажем, что можно построить n элементов
- произвольный базис Е (U). Докажем, что можно построить n элементов 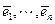 , линейно выражающихся через
, линейно выражающихся через 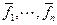 и образующих ОНБ. Используем индукцию по n. При n =1 утверждение очевидно: достаточно взять любой вектор
и образующих ОНБ. Используем индукцию по n. При n =1 утверждение очевидно: достаточно взять любой вектор 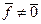 и положить
и положить
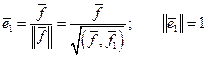 .
.
Убедимся в том, что если для n- 1 построена последовательность ортонормированных элементов 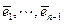 , то следующий элемент
, то следующий элемент 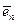 можно вычислить по формуле
можно вычислить по формуле
Пусть в (n -1)-мерном ЕП(УП) существует ОНБ; покажем, что ОНБ существует и в n -мерном E(U). Линейная оболочка 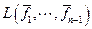 является (n -1)-мерным пространством и в нем по индуктивному предположению существует ОНБ
является (n -1)-мерным пространством и в нем по индуктивному предположению существует ОНБ 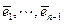 . Так как
. Так как 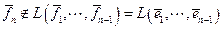 , то вектор
, то вектор 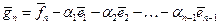 отличен от нулевого вектора при любых
отличен от нулевого вектора при любых 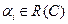 . Будем выбирать коэффициенты
. Будем выбирать коэффициенты 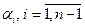 из условия ортогональности вектора
из условия ортогональности вектора 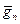 всем векторам
всем векторам 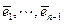 :
: 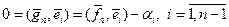 , или
, или 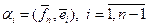 .
.
Тогда, положив 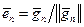 , получим ОНБ
, получим ОНБ 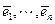 пространства E(U). #
пространства E(U). #
Алгоритм построения по данной системе n линейно независимых элементов 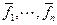 системы n попарно ортонормированных элементов
системы n попарно ортонормированных элементов 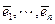 называется процессом ортогонализации Грамма-Шмидта. Он состоит в следующем:
называется процессом ортогонализации Грамма-Шмидта. Он состоит в следующем:
Первый шаг. Полагая 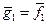 находим
находим 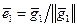 .
.
k-й шаг (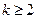 ). Полагаем
). Полагаем
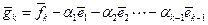 , (3.8)
, (3.8)
где 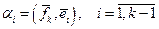 , и находим
, и находим 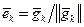 .
.
Через n шагов получим ОНБ 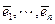 пространства.
пространства.
Более подробно:
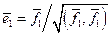 ,
,
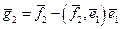 ,
, 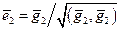 ,
,
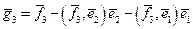 ,
, 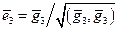 ,
,
……………………………………………………………….
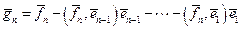 ,
, 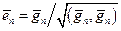 .
.
Матрица Грама
Матрицей Грама системы векторов  ЕП(УП) называется матрица
ЕП(УП) называется матрица
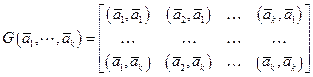 . (4.1)
. (4.1)
Определитель матрицы Грама называется определителем Грама.
Т е о р е м а. Система векторов  ЕП(УП) линейно зависима тогда и только тогда, когда
ЕП(УП) линейно зависима тогда и только тогда, когда 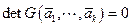 .
.
Д о к а з а т е л ь с т в о. Необходимость. Пусть  . -линейно зависимая система векторов. Последовательно умножая нетривиальную линейную комбинацию
. -линейно зависимая система векторов. Последовательно умножая нетривиальную линейную комбинацию
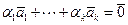 (4.2)
(4.2)
скалярно на векторы  , получим однородную систему уравнений относительно неизвестных
, получим однородную систему уравнений относительно неизвестных 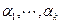 :
:
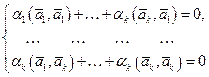 (4.3)
(4.3)
с матрицей коэффициентов 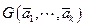 . Из существования нетривиального решения полученной системы уравнений следует, что
. Из существования нетривиального решения полученной системы уравнений следует, что 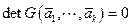 .
.
Достаточность. Пусть 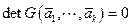 . Тогда система имеет нетривиальное решение
. Тогда система имеет нетривиальное решение 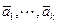 . Перепишем систему в виде
. Перепишем систему в виде
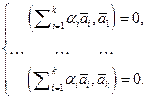 (4.4)
(4.4)
Это значит, что вектор 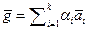 , с одной стороны, принадлежит
, с одной стороны, принадлежит 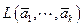 , а с другой стороны, ортогонален
, а с другой стороны, ортогонален 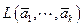 . Согласно аксиоме 4) скалярного произведения вектор
. Согласно аксиоме 4) скалярного произведения вектор 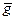 может быть только нулевым. Значит, для векторов
может быть только нулевым. Значит, для векторов  имеет место соотношение, откуда с учетом нетривиальности набора
имеет место соотношение, откуда с учетом нетривиальности набора 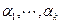 следует линейная зависимость векторов
следует линейная зависимость векторов  . #
. #
О п р е д е л е н и е. Матрица 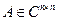 называется эрмитовой матрицей, если
называется эрмитовой матрицей, если
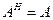 . (4.5)
. (4.5)
Матрица 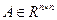 называется симметрической матрицей, если
называется симметрической матрицей, если
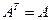 . (4.6)
. (4.6)
Т е о р е м а. Матрица Грамма системы векторов ЕП(УП) эрмитова.
Д о к а з а т е л ь с т в о. Пусть 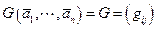 . Из (4.1) следует, что
. Из (4.1) следует, что 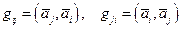 , т.е.
, т.е. 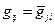 . Это означает, что
. Это означает, что 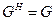 или, в вещественном случае
или, в вещественном случае 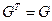 . #
. #
Т е о р е м а. Определитель Грамма линейно независимой системы векторов в ЕП(УП) положителен.
Д о к а з а т е л ь с т в о.. Пусть  линейно независимая система векторов ЕП(УП). Тогда
линейно независимая система векторов ЕП(УП). Тогда 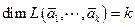 . Выберем ОНБ
. Выберем ОНБ 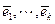 линейной оболочки
линейной оболочки 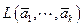 . Составим матрицу
. Составим матрицу
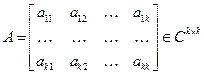
столбцами которой являются координаты векторов  в базисе
в базисе 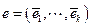 . Тогда
. Тогда
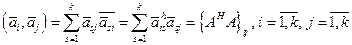 . Следовательно,
. Следовательно,
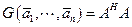 (4.7)
(4.7)
и 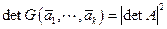 . Таким образом,
. Таким образом,
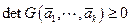 . (4.8)
. (4.8)
Так как система  линейно независима, то
линейно независима, то 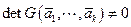 . Отсюда с учетом (4.7) следует, что
. Отсюда с учетом (4.7) следует, что 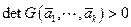 . #
. #
Замечание. В вещественном случае Матрица Грама запишется в виде
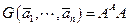 .
.
 2020-05-11
2020-05-11 247
247








