Из теоремы следует, что задача о перпендикуляре имеет, и притом единственное, решение. Укажем один из способов построения этого решения.
Пусть 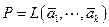 . Разложение
. Разложение 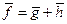 равносильно задаче построения векторов
равносильно задаче построения векторов 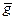 и
и 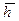 таких, что
таких, что
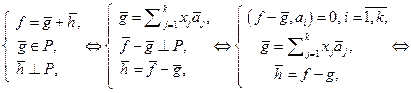
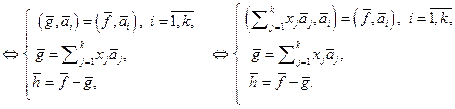
Итак, задача о перпендикуляре сводится к поиску чисел 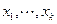 , для которых
, для которых
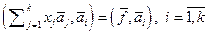 . (5.4)
. (5.4)
Сравнение этих соотношений с(5.3) и (5.4) говорит о том, что числа 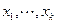 являются решением системы с матрицей Грамма
являются решением системы с матрицей Грамма 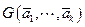 и правой частью
и правой частью 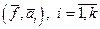 .
.
Отметим возможные при этом варианты.
1. Если 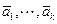 - ОНБ P, то
- ОНБ P, то 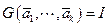 и система () имеет единственное решение
и система () имеет единственное решение 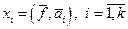 , при этом
, при этом 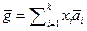 ,
, 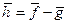 .
.
2. Если 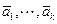 - линейно независимы, то
- линейно независимы, то 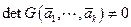 и система (5.4) имеет единственное решение; решив систему (), найдем
и система (5.4) имеет единственное решение; решив систему (), найдем 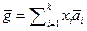 ,
, 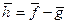 .
.
3. Если 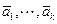 - линейно зависимы, то
- линейно зависимы, то 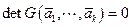 и система (5.4) имеет бесконечно много решений, которые соответствуют бесконечному числу разложений вектора
и система (5.4) имеет бесконечно много решений, которые соответствуют бесконечному числу разложений вектора 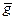 по линейно зависимой системе векторов
по линейно зависимой системе векторов 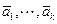 .
.
 2020-05-11
2020-05-11 199
199








