Разложение евклидова пространства

1 2 3 4 5 6 7

Пусть P - ЛПП в ЕП Е (в УП U).

О п р е д е л е н и е. Вектор называется ортогональным к подпространству , если он ортогонален любому элементу :

Т е о р е м а.

1) тогда и только тогда, когда .

2) Если .

3) Если .

4) Если (теорема Пифагора).

5) Если ненулевые векторы попарно ортогональны, т.е. , то они линейно независимы.

Д о к а з а т е л ь с т в о.

1), 2), 3) – доказать самостоятельно.

4. и в силу аксиом и определения нормы имеем

5. Рассмотрим линейную комбинацию векторов , равную нулевому вектору

Умножая скалярно это равенство на вектор , получаем , что и требовалось.

Пусть P – произвольное ЛПП n -мерного ЕП Е: .

О п р е д е л е н и е. Совокупность всех элементов , каждый из которых ортогонален подпространству Р, называется ортогональным дополнением подпространства P и обозначается .

Т е о р е м а. Ортогональное дополнение к подпространству является линейным подпространством.

Д о к а з а т е л ь с т в о. Пусть , тогда и для . Далее , т.е. . Аналогично, если , то 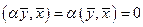, т.е. . Отсюда следует, что - линейное подпространство.

Т е о р е м а. Если P – линейное подпространство , то

(5.1)

Д о к а з а т е л ь с т в о. Утверждение очевидно, если P – тривиальное подпространство.

Пусть P -нетривиальное подпространство. Выберем ОНБ в P и ОНБ в . Система векторов ортонормирована и, следовательно, линейно независима. Покажем, что она образует базис всего пространства . Пусть это не так. Тогда существует вектор , который не является линейной комбинацией векторов . Система векторов линейно независима, и применение к ней процесса ортогонализации приводит к вектору , который ортогонален и, значит, . 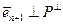С другой стороны, , так как ортогонален . Следовательно, . Отсюда вытекает линейная зависимость векторов , что противоречит допущению. Таким образом, система векторов является базисом и . Так как , то согласно теореме получаем . #

Следствие. Если L – линейное подпространство , то для существует, и притом единственное, разложение

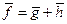, (5.2)

где .

Вектор называется ортогональной проекцией (ОП) вектора на подпространство Р, а вектор - ортогональной составляющей вектора .

Задачу разложения вектора на ортогональную проекцию и ортогональную составляющую называют задачей о перпендикуляре. По аналогии с геометрией ортогональную составляющую называют перпендикуляром, опущенным из вектора на подпространство P, а сам вектор - наклонной к подпространству P.