Ортогональные векторы

О п р е д е л е н и е.   Элементы 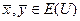 называются ортогональными (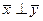), если .

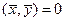Система векторов 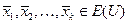называется ортогональной системой, если

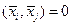при 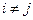.                                    (3.1)

Система векторов 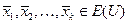 называется ортонормированной системой, если

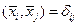, где 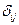 символ Кронекера, т.е.

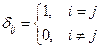                                                   (3.2)

Т е о р е м а 3.1. Ортогональная система ненулевых векторов линейно независима.

Доказательство. Пусть 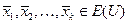 - ортогональная система ненулевых векторов. Умножая обе части равенства

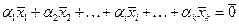                                (3.3)

скалярно на 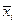 получим

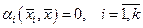.                                            (3.4)

По условию 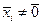,значит 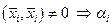, т.е. все коэффициенты линейной комбинации равны нулю. Следовательно, векторы рассматриваемой системы линейно независимы. #

Следствие 1. Ортонормированная система векторов линейно независима.

Следствие 2. В n -мерном ЕП(УП) любая ортонормированная система из n векторов образует базис.

 Ортонормированные базисы.

В ЛП все базисы равноправны. В ЕП(УП) существуют специальные, наиболее удобные базисы, называемые ортонормированными.

О п р е д е л е н и е. Базис 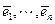 в ЕП (УП) называется ортонормированным (ОНБ), если элементы этого базиса попарно ортогональны и норма каждого из этих элементов равна единице:

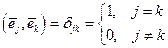.                                               (3.5)