О п р е д е л е н и е. Множество М называется метрическим пространством, если задано отображение
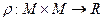
которое каждой упорядоченной паре элементов 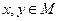 ставит в соответствие число
ставит в соответствие число  такое, что:
такое, что:
1)  ,
,  ,
, 
2)  ,
,  ,
,
3) 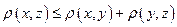 ,
,  ,
,
Число  называется расстоянием между x и y; отображение
называется расстоянием между x и y; отображение  - метрикой, аксиомы 1)-3) – аксиомами метрики(расстояния).
- метрикой, аксиомы 1)-3) – аксиомами метрики(расстояния).
О п р е д е л е н и е. Расстоянием между множествами X и Y в метрическом пространстве называется число
 . (6.1)
. (6.1)
Т е о р е м а. В евклидовом(унитарном) пространстве Vправило
 (6.2)
(6.2)
задает метрику.
Д о к а з а т е л ь с т в о. Действительно, правило (6.2) определяет отображение  , которое отвечает всем аксиомам метрики. Проверка аксиом тривиальна, отметим только одну из них:
, которое отвечает всем аксиомам метрики. Проверка аксиом тривиальна, отметим только одну из них:
 ,
,  . #
. #
Итак, Е(U) пространство является метрическим пространством относительно метрики (6.2).
Т е о р е м а. (о кратчайшем расстоянии). Расстояние между вектором  и линейным подпространством P в евклидовом(унитарном) пространстве равно длине перпендикуляра, опущенного из вектора
и линейным подпространством P в евклидовом(унитарном) пространстве равно длине перпендикуляра, опущенного из вектора  на P.
на P.
Д о к а з а т е л ь с т в о. Пусть  , где
, где 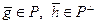 , и
, и  - произвольный вектор из P. Тогда
- произвольный вектор из P. Тогда  . Отсюда следует, что
. Отсюда следует, что  и
и 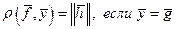 . Это означает, что
. Это означает, что  . #
. #
Эта теорема может быть переформулирована также и в других терминах:
1) расстояние между вектором  и подпространством Р равно расстоянию между вектором
и подпространством Р равно расстоянию между вектором  и его ортогональной проекцией на Р;
и его ортогональной проекцией на Р;
2) среди всех векторов подпространства Р ближе всего к вектору  расположена его ортогональная проекция на Р.
расположена его ортогональная проекция на Р.
 2020-05-11
2020-05-11 132
132








