ЛЕКЦИЯ 2 (продолжение)
Теорема. Вероятность появления хотя бы одного события.
Вероятность появления хотя бы одного из событий A1, A2,… An находится по формуле:
P (A1 + A2 +…+ An) = 1 - P 
Доказательство
Пусть событие A заключается в появлении хотя бы одного из событий
A1, A2,… An . Тогда A = A1 + A2 +…+ An.
Рассмотрим противоположное событие  - не произошло ни одно из
- не произошло ни одно из
событий A1, A2,… An. Тогда  =
=  . Следовательно,
. Следовательно,
P(A) = 1 – P( ) = 1 – P(
) = 1 – P( ).
).
Определение. Надежностью элемента называется вероятность его
безотказной работы в течение определенного промежутка времени.
Пример. Определить надежность схемы, если надежности элементов А  , А
, А  , А
, А  , А
, А 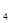 и А
и А  , работающих независимо, соответственно равна
, работающих независимо, соответственно равна
0,6; 0,4;0,5; 0,3 и 0,9.

Решение.
Пусть событие А – схема работает. Тогда
А = А  · (А
· (А  + А
+ А  +А
+А 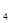 ) ·А
) ·А 
Поэтому Р(А) = Р(А  (А
(А  + А
+ А  +А
+А 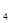 ) А
) А  ) =
) =
по теореме умножения независимых событий
= Р(А  )·Р(А
)·Р(А  + А
+ А  +А
+А 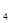 )· Р(А
)· Р(А  ) =
) =
по теореме о вероятности появления хотя бы одного события
= Р(А  )· (1 - P
)· (1 - P  )·Р(А
)·Р(А  ) =
) =
по теореме умножения независимых событий
= Р(А  )· (1 -
)· (1 -  )·Р(А
)·Р(А  ) = 0,6·(1 – 0,6·0,5·0,7)·0,9 =0,43
) = 0,6·(1 – 0,6·0,5·0,7)·0,9 =0,43
Статистическое определение вероятности
На основании опыта мы считаем более вероятными те события, которые происходят чаще, менее вероятными – которые происходят реже. Таким образом, понятие вероятности события в самой своей основе связано с практическим понятием частоты события.
Определение. Частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов:
Pn 
Частоту события часто называют его статистической вероятностью. При небольшом количестве опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Однако при увеличении числа опытов частота события все более теряет свой случайный характер, проявляет тенденцию стабилизироваться.
Пример. Опыт Бюффона.
Французский естествоиспытатель Жорж-Луи Бюффон (1707 – 1788) бросил монету 4040 раз, герб выпал 2048 раз. Частота появления герба

Схема независимых испытаний Бернулли
Проводится n независимых опытов, в каждом из которых может произойти (с вероятностью р) или не произойти (с вероятностью 1 – р = q) некоторое событие А, т.е. производится n независимых испытаний Бернулли. Такие повторные независимые испытания Бернулли называют схемой Бернулли (в честь швейцарского математика Якоба Бернулли 1654 – 1705, который доказал важную теорему, относящуюся к таким испытаниям).
Опыты являются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.
Примеры независимых испытаний.
1. Несколько последовательных бросаний монеты.
2. Несколько последовательных выниманий карты их колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются.
Формула Бернулли.
Теорема.
Проводится n независимых опытов, в каждом из которых может произойти или не произойти некоторое событие А. Вероятность появления события А (успех испытания) в каждом опыте Р(А) = р. Вероятность непоявления события А (неуспех испытания) в каждом опыте Р(Ā) = q = 1 - р. Тогда вероятность того, что при n испытаниях Бернулли будет k «успехов» находится по формуле Бернулли:
Рn(k) =  рk qn-k.
рk qn-k.
Доказательство.
Рассмотрим событие Вk, состоящее в том, что событие А появится при n испытаниях ровно kраз.
Будем обозначать через Аiпоявление, а через Āi - не появление события А в i-ом эксперименте, Р(Аi) = р, Р(Āi) = q. События А1, А2 , …,Аn независимы.
Каждый способ реализации события Вk (т.е. каждый член суммы разложения события Вk) должен состоять из k появлений события А и n – k не появлений, т.е.
Вk = А1А2 … Аk Āk+1 … Ān + … + Ā1 Ā2 … Ān-k Аn-k+1 … Аn,
При этом в каждое такое произведение событие Аi должно входить k раз, а событие Āj - n – k раз.
Число всех комбинаций такого рода равно числу способов 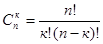 выбора k экспериментов, в которых осуществлялось событие А, из n экспериментов. Вероятность каждой такой комбинации по теореме умножения для независимых событий, равна рkqn-k. Так как эти комбинации между собой несовместны, то по теореме сложения вероятность события Вk равна
выбора k экспериментов, в которых осуществлялось событие А, из n экспериментов. Вероятность каждой такой комбинации по теореме умножения для независимых событий, равна рkqn-k. Так как эти комбинации между собой несовместны, то по теореме сложения вероятность события Вk равна
Рn(k) =  рk qn-k.
рk qn-k.
Следствие. Вероятность того, что событие А появится не менее m 1 и не более m 2 раз при n испытаниях Бернулли определяется по формуле
 .
.
Локальная теорема Муавра – Лапласа
Формула Бернулли Рn(k) =  рk qn-kнеудобна при больших значениях n; поэтому, вероятность в этом случае вычисляют по приближенной формуле.
рk qn-kнеудобна при больших значениях n; поэтому, вероятность в этом случае вычисляют по приближенной формуле.
Теорема (локальная теорема Муавра-Лапласа). Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A произойдёт k раз в n независимых испытаниях при достаточно больших значениях n, приближённо равна
Рn(k) =  рk qn-k
рk qn-k  ,
,
где
 ;
; 
(без доказательства).
Локальную теорему Муавра-Лапласа применяют, если выполнено условие n×p×q ³ 20.
Значения функции j (x) можно вычислить на калькуляторе или найти с помощью таблицы, приведенной в Приложении 1 (Гмурман). При этом следует иметь в виду, что j (x) чётная функция, значит, j (-x) = j (x). Можно также считать, что, если x > 4, то j (x) = 0.
Пример. Вычислить вероятность того, что при 100-кратном бросании монеты орёл выпадет ровно 60 раз.
Решение. Имеем n = 100; p = 0,5; q = 0,5. Условие n×p×q = 100×0,5×0,5 = 25 ³ 20 выполнено. Применим формулу Муавра-Лапласа
Р100(60)≈ 
Ответ: 0,0108.
Интегральная теорема Муавра-Лапласа
Теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события A постоянна и равна p (0 < p < 1) событие A наступит не менее m 1 и не более m 2 раз приближённо равна
P (m 1, m 2) = F(x 2) - F(x 1).
Здесь
F(x) =  - функция Лапласа,
- функция Лапласа,
x 1 = (m 1 – np)/  , x 2 = (m 2 – np)/
, x 2 = (m 2 – np)/  .
.
Таблица значений функции Лапласа F(x) для положительных значений x (0 ≤ x ≤ 5) приведена в Приложении 2 (Гмурман). При этом следует иметь в виду, что F(x) нечётная функция, поэтому F(-x) = - F(x). Можно также считать, что, если x > 5, то F(x) = 0,5.
Пример. Вычислить вероятность того, что при 100-кратном бросании монеты орёл выпадет не менее 40 и не более 60 раз.
Решение. Имеем n = 100; p = 0,5; q = 0,5; m 1 = 40; m 2 = 60.
Применим интегральную формулу Муавра-Лапласа
P (40, 60) = F(x 2) - F(x 1),
где F(x) - функция Лапласа,
x 1 = (40 - 100×0,5)/  = -2,
= -2,
x 2 = (60 - 100×0,5)/  = 2.
= 2.
Учитывая, что функция Лапласа нечётная функция, получим
P (40 ≤ m ≤ 60) = F (2) - F (-2) = 2 F (2).
По таблице Приложения 2 (Гмурман) находим F (2) = 0,4772.
Значит,
P (40 ≤ m ≤ 60) = 2×0,4772 = 0,9545.
Ответ: 0,9545.
Формула Пуассона
Если вероятность p наступления события A в каждом испытании есть малое число, а число испытаний n - велико, то формула Бернулли становится громоздкой и непригодна для вычислений. В этом случае вычисления выполняют по приближенной формуле Пуассона.
Теорема. Если вероятность p наступления события A в каждом испытании стремится к нулю (p ®0) при неограниченном увеличении числа n испытаний (n ®¥), причём произведение np стремится к постоянному числу l (np ® l), то вероятность Рn(k) =  рk qn-k того, что событие A появится k раз в n независимых испытаниях, удовлетворяет приближённому равенству
рk qn-k того, что событие A появится k раз в n независимых испытаниях, удовлетворяет приближённому равенству
Рn(k)  ,
,
где l = n×p.
Эта формула называется формулой Пуассона
Пример: На факультете насчитывается 1606 студентов. Какова вероятность того, что 23 апреля является днём рождения одновременно 5 студентов?
Решение: Применим формулу Пуассона потому, что вероятность
p = 1/365 - мала, а число n = 1606 - велико. Вычислим l = np; l = 1606/365 =4,4. Положим в формуле Пуассона k = 5, l = 4,4; в результате получим
Р1606(5)  =
= 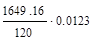 = 0,169.
= 0,169.
Ответ: 0,169.
ЛЕКЦИЯ № 3
 2020-05-11
2020-05-11 337
337







