Определение. Случайная величина называется непрерывной, если существует неотрицательная функция f(x) такая, что при любом x
FX (x) = P{ X < x } = 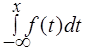 .
.
Функция распределения непрерывной случайной величины вcюду дифференцируема, причем ее производная равна F´(x) = fX(x).
Из равенства P{X = x } = FX(x+0) – FX(x) следует, что вероятность любого отдельного значения X = x непрерывной случайной величины равна нулю.
Определение. Функцию f(x) называют плотностью распределения случайной величины Х.
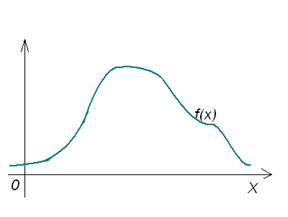 Кривая, являющаяся графиком плотности распределения случайной величины, называется кривой распределения. Геометрически F(x) представляет собой площадь под кривой распределения, лежащую
Кривая, являющаяся графиком плотности распределения случайной величины, называется кривой распределения. Геометрически F(x) представляет собой площадь под кривой распределения, лежащую
лежащую левее точки х.
Используя формулу Ньютона – Лейбница, можно записать вероятность попадания случайной величины в заданный интервал (а,b) через плотность распределения:
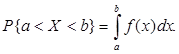
Так как вероятность любого отдельного значения непрерывной случайной величины равна нулю, то здесь можно рассматривать открытый интервал, не включая в него левый конец а. В частности, интеграл по всей числовой оси от плотности распределения равен единице:
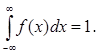
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Функция распределения случайной величины, плотность распределения, а также ряд распределения, являются исчерпывающими характеристиками случайной величины.
Однако во многих практических приложениях нет необходимости приводить исчерпывающее описание случайной величины. Зачастую достаточно указать только отдельные числовые параметры, характеризующие основные черты распределения случайной величины: например, среднее значение, около которого группируются все возможные значения случайной величины, а также какую-либо величину, характеризующую степень разбросанности этих значений относительно среднего. Пользуясь такими характеристиками, все существенные сведения о случайной величине можно выразить достаточно компактно. Указанные характеристики называют числовыми характеристиками случайной величины.
В теории вероятностей числовые характеристиками и операции с ними играют большую роль. Часто удается решить практическую задачу до конца, оставляя в стороне законы распределения и используя только числовые характеристики.
1.Математическое ожидание случайной величины
Среднее значение случайной величины – некоторое число, являющееся как бы её представителем и заменяющее случайную величину при грубо ориентировочных расчетах. Когда говорят «средняя продолжительность жизни в России равна 60 годам» или «средняя заработная плата в городе N равна 3000 руб.», то этим указывают определенную числовую характеристику случайной величины, описывающую её положение на числовой оси, т.е. характеристику положения.
Из характеристики положения в теории вероятностей важнейшую роль играет математическое ожидание (или среднее значение) случайной величины.
Определение. Рассмотрим дискретную случайную величину Х, принимающую возможные значения х1, х2, х3, …, с вероятностями р1, р2, р3, …. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:
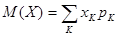 .
.
Для непрерывной случайной величины Х с плотностью f(x) математическое ожидание выражается уже не суммой, а интегралом:
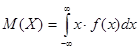 .
.
Заметим, что математическое ожидание существует не для всех случайных величин, так как сумма и интеграл в определении должны сходиться.
Перечислим простейшие свойства математического ожидания:
1 ) математическое ожидание постоянной равно этой постоянной:
M(C) = C;
2) постоянную величину можно выносить за знак математического ожидания, т.е. М(С·Х) = С·M(Х).
3) M(X + Y) = MX + MY
2. Медиана и мода случайной величины
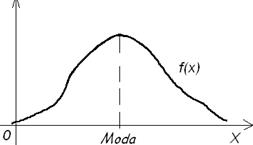
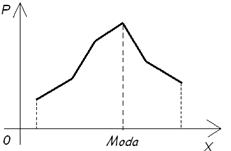 Кроме важнейшей из характеристик положения, математического ожидания, на практике применяют другие характеристики положения, в частности, моду и медиану случайной величины. Модой дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной величины модой является то значение, в котором плотность вероятности максимальна.
Кроме важнейшей из характеристик положения, математического ожидания, на практике применяют другие характеристики положения, в частности, моду и медиану случайной величины. Модой дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной величины модой является то значение, в котором плотность вероятности максимальна.
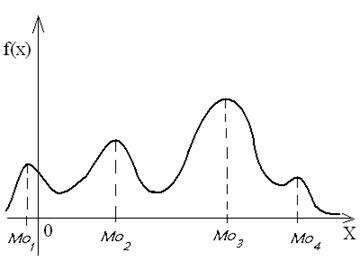 Если многоугольник распределения или кривая распределения имеют более одного максимума, то распределение называют полимодулярным.
Если многоугольник распределения или кривая распределения имеют более одного максимума, то распределение называют полимодулярным.
Если же многоугольник распределения или кривая распределения имеют ровно один максимум, то распределение называют унимодулярным.
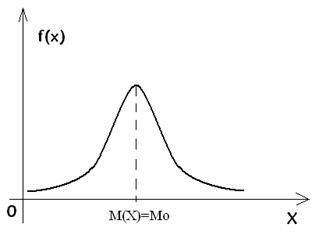 В общем случае математическое ожидание и мода не совпадают. В случае, когда распределение является симметричным и существуют мода и математическое ожидание, то они совпадают друг с другом, а также с центром симметрии распределения.
В общем случае математическое ожидание и мода не совпадают. В случае, когда распределение является симметричным и существуют мода и математическое ожидание, то они совпадают друг с другом, а также с центром симметрии распределения.
На рисунке – кривая симметричного унимодального распределения.
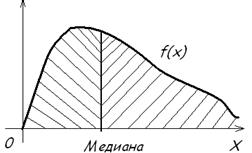 Для непрерывных случайных величин применяют ещё одну характеристику положения - медиану случайной величины. Медиана - это абсцисса точки, в которой площадь под кривой распределения делиться пополам, т.е. одинаково вероятно, окажется ли случайная величина меньше или больше медианы.
Для непрерывных случайных величин применяют ещё одну характеристику положения - медиану случайной величины. Медиана - это абсцисса точки, в которой площадь под кривой распределения делиться пополам, т.е. одинаково вероятно, окажется ли случайная величина меньше или больше медианы.
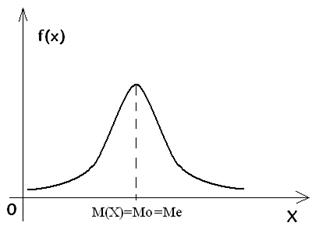 В случае симметричного унимодального распределения медиана совпадает с математическим ожиданием и модой.
В случае симметричного унимодального распределения медиана совпадает с математическим ожиданием и модой.
 2020-05-11
2020-05-11 398
398








