2020-05-11
469
Формулировка (прямая теорема): если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.
(Доказательство прямой теоремы)
доказательства теоремы о трёх перпендикулярах с помощью векторов. Этот способ не требует специального расположения прямой, проведённой на плоскости перпендикулярно наклонной или её проекции. Совсем необязательно, чтобы прямая на плоскости проходила через основание наклонной; главное, чтобы она была перпендикулярна этой наклонной.
Вот этот способ.
Дано:
Плоскость α
SO ┴ α
SA – наклонная
OA – проекция SA
MN принадлежит α
Доказать:
MN ┴ SA
Доказательство:
Зададим векторы 
, 
, 
, 
.
= +
Умножим обе части на :
• = • + •
Скалярное произведение двух перпендикулярных векторов равно 0:
• = 0, но и не нулевые векторы, значит, ┴ , прямая оказалась перпендикулярной наклонной, что и требовалось доказать.
ВЕКТОРНОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ Пифагора:
Пусть АВС - прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b + c = a
откуда имеем
c = a - b
возводя обе части в квадрат, получим
c²=a²+b²-2ab
Так как a перпендикулярно b, то ab=0, откуда
c²=a²+b² или c²=a²+b²
Теорема Пифагора снова доказана.
Если треугольник АВС - произвольный, то та же формула дает т. н. теорему косинусов, обобщающую теорему Пифагора.
Теорема косинусов для треугольника.
|
|
|
Во всяком треугольнике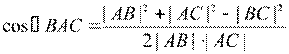 
,
. 
Доказательство:
Рассмотрим векторное равенство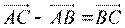 
. Возьмем скалярный квадрат:
,
,
.
Пусть 
- единичный вектор, отложенный от точка А на луче [АВ), 
- единичный вектор, отложенный от точки А на луче [АС). Тогда
.
Отсюда
,
.
Практические задания
- Доказать теорему о перпендикулярности прямой и плоскости.
- Дана пирамида АВСD, все грани которой – правильные треугольники. Докажите, что скрещивающиеся ребра взаимно перпендикулярны.
УЧЕБНАЯ КАРТА ПРАКТИЧЕСКОГО ЗАНЯТИЯ №12
| Дата | Группа |
| 1111 | |
| 1211 | |
| 1311 | |
| 1411 | |
| 1511 |
