Практические задания

Задание 1.

1.Составить уравнение прямой, проходящей через точку А(2; —1) и имеющей направляющий вектор n = (— 4; 2).

2.Составить уравнение прямой, проходящей через точку С(2; —2) и имеющей направляющий вектор n = (3; -2).

3.Составить уравнение прямой, проходящей через точку М(2; —3) и имеющей направляющий вектор n = (— 4; 5).

4.Составить уравнение прямой, проходящей через точку В(4; —3) и имеющей направляющий вектор n = (7; -3).

5.Составить уравнение прямой, проходящей через точку С(-6; —2) и имеющей направляющий вектор n = (— 4; 1).

Задание 2. Составить уравнения прямых, заданных двумя точками:

1. А(1; 3). B(4;1).

2. С(-1; 5). D(3; -7).

3. Q(-3; 0), N(0; 5).
4. P(0; 0), O(-3; 5).
5. C(7;-1),S(-1;-1).

 

Задание 3.

1.Составить уравнение плоскости, проходящей через точку М₀(-1;3; 2 ) перпендикулярно вектору п = (2; -3; 4 )

2.Составить уравнение плоскости, проходящей через точку М₀(2;-3; -1 ) перпендикулярно вектору п = (3; 1; -2 )

3.Составить уравнение плоскости, проходящей через точку М₀(1;5;- 2 ) перпендикулярно вектору п = (1; -7; 5 )

4.Составить уравнение плоскости, проходящей через точку М₀(4;-6; 3 ) перпендикулярно вектору п = (-1; -2; 4 )

5.Составить уравнение плоскости, проходящей через точку М₀(-1;4; 5 ) перпендикулярно вектору п = (3; -1; 7 )

 

 

                                                                

 

 УЧЕБНАЯ КАРТА ПРАКТИЧЕСКОГО ЗАНЯТИЯ №13

Дата	Группа
	1111
	1211
	1311
	1411
	1511

Наименование учебной дисциплины

  ОУДП.12 Математика

Наименование темы учебной дисциплины Тема 3.3

Многогранники и их поверхности.

  Тема практического занятия:   Построение сечений многогранников, вычисление их площадей

Количество часов:   2 часа   

Место проведения:  Кабинет Математики

Характер работы:  репродуктивный

Форма организации учебной деятельности студентов: индивидуальная

Образовательные задачи:

o Обобщение, закрепление теоретических знаний:

- правила построения сечений многогранников, 

- формулы площадей: треугольника, параллелограмма, трапеции, многоугольника.

o Формирование умений:

- построение сечений многогранников,

- вычисление их площадей;

- решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

3) Формирование интеллектуальных и исследовательских умений:

- выделять главное, существенные признаки;

- осуществлять самоконтроль и коррекцию своей учебной деятельности;

- рационально использовать рабочее время.

4) Формирование компонентов компетенций

- способность к самостоятельному поиску истины

 

Оборудование (аппаратура, материалы и др.):

– раздаточный материал, тексты заданий;

- ПК и медиаоборудование;

- компьютерная презентации в среде Power Point: Построение сечений в параллелепипеде. Построение сечений в пирамиде.

 

  Задание студентам на самоподготовку (учебная и справочная литература):

Богомолов Н.В. Сборник дидактических заданий, Задание 50, с. 149-150

Хронологическая структура заданий практического занятия

Время (мин)	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90
Структурные элементы	1	2	2	2	3	3	3	4	4	4	4	4	4	4	4	4	5	5

 

ДИДАКТИЧЕСКАЯ СТРУКТУРА ЗАНЯТИЯ

Структурные элементы	Деятельность преподавателя	Деятельность студентов
1. Целевая установка.	1. Сообщение плана учебного занятия. 2. Ознакомление с требованиями к знаниям и умениям по теме.	1. Подготовка рабочего места 2. Запись темы урока.
2. Проверка теоретической готовности студентов к выполнению заданий практического занятия	Проверка домашнего задания: 1) проверка выполнения решения задач №№…. (в рабочих тетрадях) 2) организация фронтального опроса 3) организация индивидуального опроса (у доски) – решение типовой задачи с объяснением алгоритма действий	Демонстрируют выполнение домашнего письменного задания Отвечают на вопросы Решают задачу. Объясняют алгоритм решения
3. Инструктаж о содержании, этапах работы, способах (методах) действий.	1) Сообщение содержания и последовательности выполнения практических заданий 2) Представление комплектов материалов, необходимых для выполнения заданий (учебник, компьютерная презентация, раздаточный материал) 3) Обучение практическим приемам:   построения сечений многогранников, вычисление их площадей; решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике на примере решения типовой задачи	1) Подготовка к выполнению практических заданий 2) Ознакомление с комплектом учебных материалов 3) Усвоение правил работы:  построения сечений многогранников, вычисление их площадей; решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике на примере решения типовой задачи
4. Организация выполнения заданий практического занятия	1) Организация выполнения студентами практических заданий:  Задание 1. построение сечений в параллелепипеде   Задание 2. построению сечений в пирамиде. 2) Выявление и устранение возникающих у студентов затруднений в процессе решения задач. Организация работы над основными математическими понятиями: Правила построения сечений многогранников, знать формулы площадей: треугольника, параллелограмма, трапеции, многоугольника.	Самостоятельная работа студентов по выполнению заданий
5. Оценка выполненной работы	1) Проверка правильности выполнения заданий 2) Оценка результатов выполнения заданий	Ответы на поставленные вопросы, пояснения полученных результатов.

Основные понятия

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Пример 1.

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

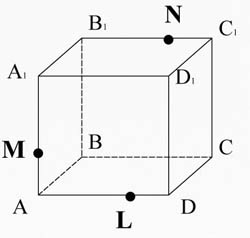
Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML (принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К. Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

 

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Точки X₂ и X₃ лежат в плоскости DD₁C₁C. Проведем прямую X₂ X₃, которая пересечет ребро C₁C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL - искомое сечение.

Пример 2. Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML (принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM (они лежат в параллельных плоскостях).

.

Соединим точки P и L (они лежат в одной плоскости).

.

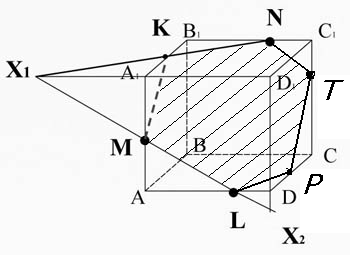MKNTPL - искомое сечение.

Соединим точки М и L, лежащие в плоскости  AA₁D₁D

Примеры задач.

 

1. Постройте сечение куба плоскостью проходящей через точки, указанные на рисунке

2. Постройте сечение правильной четырехугольной пирамиды плоскостью, через точки, указанные на рисунке.

 

Решение:

1)

А) проводим линию пересечения с гранью куба (АВ) Б) проводим параллельную ей (АВ)на противолежащей грани (ЕС) В) проводим ЕА Г) проводим прямую BD||EA Д) Соединяем D c C Сечение (ABDCE) построено.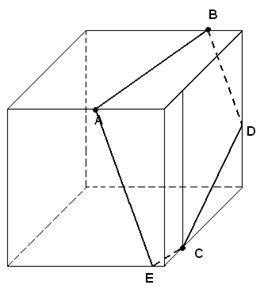

А) проецируем на плоскость основания, путем центрального проецирования из вершины, точки В и С, получая точки: B’ и C’.

Б) пересекаем прямые B’C’ и BC, находим точку P’

В) пересекаем AP’ и D’C’, находим точку D”.

Г) пересекаем D”C и SD’, находим D

ABDC – сечение.

Задача 1.

Построить сечение призмы ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже (рис.3)).

Решение.

Рис. 3

1. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА₁В₁В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.

2. Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S₁, принадлежащую следу.

3. Аналогично получаем точку S₂ пересечением прямых QR и BC.

4. Прямая S₁S₂ - след секущей плоскости на плоскость нижнего основания призмы.

5. Прямая S₁S₂ пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА₁D₁D. Аналогично получаем TU и RT.

6. PQRTU – искомое сечение.

Задача 2.

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.4)).

Решение.

Рис. 4

1. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проодящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

2. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

3. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА₁ в некоторой точке Х.

4. Точки X и N лежат в одной плоскости грани АА₁D₁D, соединим их и получим прямую XN.

5. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A₁B₁C₁D₁, параллельную прямой NP. Эта прямая пересечет сторону В₁С₁ в точке Y.

6. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

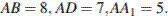За­да­ние 14 № 501752. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точк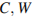и и

Ре­ше­ние.

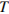От­ре­зок па­рал­ле­лен (точка при­над­ле­жит ребру ). Плос­кость се­че­ния пе­ре­се­ка­ет плос­кость по пря­мой па­рал­лель­ной сле­до­ва­тель­но, ис­ко­мое се­че­ние — па­рал­ле­ло­грамм (рис. 1).

Тре­уголь­ни­ки и равны, сле­до­ва­тель­но,

 

 

зна­чит, — ромб со сто­ро­ной и диа­го­на­лью (рис. 2). Тогда диа­го­наль

 

 

Ответ:

­Зада­ние 14 № 507319. Пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной четырёхуголь­ной пи­ра­ми­ды SABCD равна 108, а пло­щадь пол­ной по­верх­но­сти этой пи­ра­ми­ды равна 144. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ну S этой пи­ра­ми­ды и через диа­го­наль её ос­но­ва­ния.

Ре­ше­ние.

Пло­щадь ос­но­ва­ния пи­ра­ми­ды равна 144 − 108 = 36, по­это­му AB = 6. Пло­щадь бо­ко­вой грани равна Пусть SM — вы­со­та грани SAB. Тогда по­это­му SM = 9. Пусть SH — вы­со­та пи­ра­ми­ды. Имеем

 

 

Тогда

 

Ответ: 36.

За­да­ние 14 № 507596. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC угол ASB равен 36°. На ребре SC взята точка M так, что AM — бис­сек­три­са угла SAC. Пло­щадь се­че­ния пи­ра­ми­ды, про­хо­дя­ще­го через точки A, M и B, равна Най­ди­те сто­ро­ну ос­но­ва­ния.

Ре­ше­ние.

Нуж­ное се­че­ние — тре­уголь­ник AMB.

Рас­смот­рим тре­уголь­ник ASC. Он рав­но­бед­рен­ный, и Зна­чит,

Рас­смот­рим те­перь тре­уголь­ник CAM. Сумма его углов 180°, зна­чит, 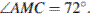Сле­до­ва­тель­но, тре­уголь­ник CAM рав­но­бед­рен­ный, и по­это­му AC=AM. Ана­ло­гич­но на­хо­дим, что BM=BC.

Таким об­ра­зом, тре­уголь­ник AMB рав­но­сто­рон­ний, и его сто­ро­на AB од­но­вре­мен­но яв­ля­ет­ся сто­ро­ной ос­но­ва­ния. По усло­вию со­ста­вим урав­не­ние от­ку­да AB = 10.

За­да­ние 14 № 501710. В пра­виль­ной четырёхуголь­ной при­зме 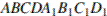сто­ро­на ос­но­ва­ния равна а бо­ко­вое ребро Точка при­над­ле­жит ребру 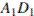и делит его в от­но­ше­нии счи­тая от вер­ши­ны 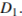Най­ди­те пло­щадь се­че­ния этой приз­мы плос­ко­стью, про­хо­дя­щей через точки 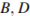и

Ре­ше­ние.

От­ре­зок па­рал­ле­лен диа­го­на­ли (точка при­над­ле­жит ребру ), сле­до­ва­тель­но, ис­ко­мое се­че­ние — тра­пе­ция 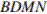(рис. 1). Плос­кость се­че­ния пе­ре­се­ка­ет ниж­нее ос­но­ва­ние no пря­мой па­рал­лель­ной зна­чит, па­рал­ле­лен

Тре­уголь­ни­к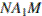и и по­доб­ны, сле­до­ва­тель­но,

Зна­чит,

В рав­ных пря­мо­уголь­ных тре­уголь­ни­ках и

зна­чит, тра­пе­ция рав­но­бед­рен­ная.

Пусть 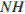— вы­со­та тра­пе­ции 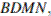про­ведённая к ос­но­ва­нию (рис. 2), тогда:

 

Ответ:

За­да­ние 14 № 504416. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC бо­ко­вое ребро SA = 5, а сто­ро­на ос­но­ва­ния AB = 4. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через ребро AB пер­пен­ди­ку­ляр­но ребру SC.

Ре­ше­ние.

В тре­уголь­ни­ке BCS про­ведём вы­со­ту BK, тогда ис­ко­мое се­че­ние — тре­уголь­ник ABK. Пусть Q — пло­щадь тре­уголь­ни­ка ABK. Се­че­ние из усло­вия раз­би­ва­ет пи­ра­ми­ду на тет­ра­эд­ры CAKB и SAKB. Их сум­мар­ный объём

 

 

равен объёму пи­ра­ми­ды.

 

Пусть — SO вы­со­та пи­ра­ми­ды. В тре­уголь­ни­ке SCO имеем:

 

 

Объём пи­ра­ми­ды SABC равен

 

 

При­рав­ни­вая два най­ден­ных зна­че­ния для объёма, по­лу­ча­ем

 

 

Ответ: .

Практические задания:

Задание 1.

Практическая задания по построению сечений параллелепипеда. Приложение 1

Приложение 2

Опора-памятка

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и причем только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом:

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Способы задания плоскости:

Приложение 3