ОУДП.12 Математика
Наименование темы учебной дисциплиныТема 3.2. Векторы и координаты
Тема практического занятия:
Решение математических и прикладных задач с использованием координат и векторов
Количество часов: 2 часа
Место проведения: Кабинет Математики
Характер работы: репродуктивный
Форма организации учебной деятельности студентов: индивидуальная
Образовательные задачи:
1) Обобщение, закрепление теоретических знаний:
- определение вектора, коллинеарных векторов, свойства координат коллинеарных векторов; действия над векторами,
- определение направляющего вектора, нормального вектора,
- формулы: уравнения прямой, заданной точкой и направляющим вектором, точкой и нормального вектором, проходящей через две данные точки,
- общее правило составления уравнения прямой l; уравнения плоскости;
- необходимые и достаточные условия параллельности прямых в прямоугольной системе координат (с помощью векторов)
2) Формирование умений:
- составлять уравнение прямой, проходящей через точку и имеющей направляющий вектор; составлять уравнение прямой, проходящей через две точки; составлять уравнение прямой, проходящей через точку параллельно прямой; составлять уравнение плоскости, проходящей через точку перпендикулярно вектору.
- векторный метод нахождения расстояния от точки до прямой ;условия параллельности прямых в прямоугольной системе координат (с помощью векторов);
- решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
3) Формирование интеллектуальных и исследовательских умений:
- выделять главное, существенные признаки;
- осуществлять самоконтроль и коррекцию своей учебной деятельности;
- рационально использовать рабочее время.
4) Формирование компонентов компетенций
- владение основами научной организации труда;
- способность к самостоятельному поиску истины.
Оборудование (аппаратура, материалы и др.):
– раздаточный материал, тексты заданий;
- ПК и медиаоборудование;
- компьютерная презентации в среде Power Point
Задание студентам на самоподготовку (учебная и справочная литература):
Башмаков М.И. Математика Глава 5, занятие 4 с. 87-88
Хронологическая структура заданий практического занятия
| Время (мин) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 |
| Структурные элементы | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
ДИДАКТИЧЕСКАЯ СТРУКТУРА ЗАНЯТИЯ
| Структурные элементы | Деятельность преподавателя | Деятельность студентов |
| 1. Целевая установка. | 1. Сообщение плана учебного занятия. 2. Ознакомление с требованиями к знаниям и умениям по теме. | 1. Подготовка рабочего места 2. Запись темы урока. |
| 2. Проверка теоретической готовности студентов к выполнению заданий практического занятия | Проверка домашнего задания: 1) проверка выполнения решения задач №№…. (в рабочих тетрадях) 2) организация фронтального опроса 3) организация индивидуального опроса (у доски) – решение типовой задачи с объяснением алгоритма действий | Демонстрируют выполнение домашнего письменного задания Отвечают на вопросы Решают задачу. Объясняют алгоритм решения |
| 3. Инструктаж о содержании, этапах работы, способах (методах) действий. | 1) Сообщение содержания и последовательности выполнения практических заданий 2) Представление комплектов материалов, необходимых для выполнения заданий (учебник, компьютерная презентация, раздаточный материал) 3) Обучение практическим приемам: составить уравнение прямой, проходящей через точку и имеющей направляющий вектор; составить уравнение прямой, проходящей через две точки; составить уравнение прямой, проходящей через точку параллельно прямой; составить уравнение плоскости, проходящей через точку перпендикулярно вектору на примере решения типовой задачи. Векторный метод нахождения расстояния от точки до прямой, условия параллельности прямых в прямоугольной системе координат (с помощью векторов) на примере решения типовой задачи. | 1) Подготовка к выполнению практических заданий 2) Ознакомление с комплектом учебных материалов 3) Усвоение правил работы: составить уравнение прямой, проходящей через точку и имеющей направляющий вектор; составить уравнение прямой, проходящей через две точки; составить уравнение прямой, проходящей через точку параллельно прямой; составить уравнение плоскости, проходящей через точку перпендикулярно вектору. Векторный метод нахождения расстояния от точки до прямой; (с помощью векторов); условия параллельности прямых в прямоугольной системе координат (с помощью векторов) на примере решения типовой задачи. |
| 4. Организация выполнения заданий практического занятия | 1) Организация выполнения студентами практических заданий: Задание 1. Составить уравнение прямой, проходящей через точку и имеющей направляющий вектор. Задание 2. Составить уравнение прямой, проходящей через две точки. Задание 3. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору. 3) Организация работы над основными математическими понятиями: вектор, коллинеарные векторы, координаты вектора; направляющий вектор, нормальный вектор, уравнения прямой, заданной точкой и направляющим вектором, точкой и нормального вектором, проходящей через две данные точки, общее правило, прямой l; уравнения плоскости; | Самостоятельная работа студентов по выполнению заданий |
| 5. Оценка выполненной работы | 1) Проверка правильности выполнения заданий 2) Оценка результатов выполнения заданий | Ответы на поставленные вопросы, пояснения полученных результатов. |
Основные понятия
Уравнение прямой, проходящей через данную точку и имеющей заданный направляющий вектор.

Направляющим вектором прямой L называется всякий ненулевой вектор n = (а; b), параллельный этой прямой. Любая прямая имеет бесконечное множество направляющих векторов, коллинеарных между собой
Пусть заданы точка М1(х1;y1), через которую проходит прямая, и ее направляющий вектор п = (а; Ь).
Используя общее правило, составим уравнение прямой L.
1°. Выберем произвольную точку М(х;y), принадлежащую прямой L.
2°. Найдем вектор М1 М = (х — х1; y — y1 ).
3°. Запишем направляющий вектор п=(а; b).
4°. Воспользуемся условием коллинеарности векторов М1 М и n; их одноименные координаты должны быть пропорциональны
Поэтому уравнение прямой L имеет вид

Преобразуем это уравнение:
bx — Ьх1 = ау — ау1;

 — уравнение общего вида.
— уравнение общего вида.
Уравнение прямой, проходящей через две данные точки.
Пусть заданы две точки М1(х1;у1) и М2(х2;у2). Через них можно провести прямую и притом только одну (см.рис.). Для составления ее уравнения воспользуемся общим правилом:
1°. Выберем на прямой l точку М(х; у).
2°, Найдем координаты вектора М1М: M1M=(x-x1)(y-y1)
3°. Найдем координаты направляющего вектора М1М2: М1М2 =(x2—x1;y2-y1)
4°. Векторы М1М и М1М2 коллинеарны. так как лежат на одной прямой, значит, искомое уравнение имеет вид

Общее уравнение плоскости.
Общее уравнение плоскости имеет вид Ах+Ву+Сz+D=0.
Уравнение плоскости, проходящей через точку М0(х0;у0; z 0) перпендикулярно заданному нормальному вектору п = (А; В;С ) имеет вид:
А(х-х 0)+В(у-у0)+С(z- z0)=0 или Ах+Ву+Сz- Ах 0 -Ву 0 -Сz 0 =0
Примеры решения задач.
Пример 1.Составить уравнение прямой, проходящей через точку А(3; —2) и имеющей направляющий вектор n = (— 5; 3).
Решение.
1°. Выбираем точку М(х; у), принадлежащую l.
2°. Найдем вектор АМ = (x - 3; y + 2).
3°Направляющий вектор n = (—5; 3).
4°Запишем уравнение прямой х-3 у+2
-5 3
откуда Зх — 9 =-5у - 10; 3x+5y+1—искомое уравнение в общем виде.
Пример 2. Треугольник задан точками А (5; 2), В(—1; —4), С(— 5, —3), Составить уравнение прямой, проходящей через точку В параллельно АС.
Решение.
1°. Выбираем точку М(х. у).
2". Найдем вектор BM = (х+1;у+4)
3°. Найдем вектор, заданный точками А (5; 2) и С(-5; -3); имеем
АС=(-10; -5)
4°. Так как искомая прямая и прямая АС параллельны, то их направляющие векторы коллинеарны. Запишем искомое уравнение прямой:

откуда х + 1 = 2y+ 8; x-2y-7=0 - искомое уравнение в общем виде.
Пример 3. Составить уравнение прямой, проходящей через точки А(2; 3) и В(7;5).
Решение. Подставив в формулу координаты данных точек, получим
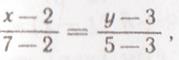

2х-5у+11=0 - искомое уравнение прямой.
Векторный метод нахождения расстояния от точки до прямой.
Введем базис 
 ,
,  .
.


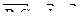
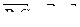

Поэтому 

Далее имеем:


Так как 
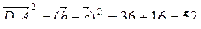



то имеем: 
Отсюда получаем:






Ответ: 
 2020-05-11
2020-05-11 104
104








