Нестандартные преобразования

· Использование формулы:  

Пример:

· Использование формулы сокращенного умножения:

Пример:

(1 + b) (1 + b ²) (1 + b ⁴) (1 + b ⁸) (1 + b ¹⁶) = (1 – b) (1 + b) (1 + b ²) (1 + b ⁴) (1 + b ⁸) (1 + b ¹⁶): (1 – b) = (1 – b ³²): (1 – b)

· Метод неопределенных коэффициентов:

Пример: найти коэффициенты aи bиз тождества:  

Решение:

Основные формулы

Примеры заданий на преобразование степеней и достаточные знания свойств, необходимые для решения этих заданий.

Задания	Достаточные знания	Формула
	Свойство степени an c натуральным показателем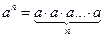
	Свойства степени произведения
	Свойства степени , основанием  которой является степень
	Свойства степени арифметического  корня
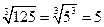
	Свойства арифметического корня с нечетным показателем 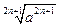 из степени с нечетным показателем
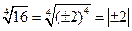
	Свойства арифметического корня с четным показателем  из степени с четным показателем
	Свойство модуля числа a
	Свойства произведения корней 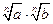 с одинаковыми показателями
	Свойства степени   с дробным показателем
	Свойства частного корней  с одинаковыми показателями
	Свойства произведения степеней  с одинаковыми основаниями
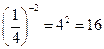
	Свойства степени  с отрицательным целым показателем
	Свойства степени  с отрицательным дробным показателем

  Примерное задание. Найдите значение выражения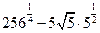

Решение:

Для решения используем последовательно знания следующих свойств:

ü Свойство степени  с дробным показателем: ;

ü Свойство степени a ⁿ c натуральным показателем: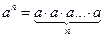

ü Свойство арифметического корня  с четным показателем степени: ;

ü Свойство произведения степеней с одинаковыми основаниями: ;

ü Свойство модуля числа: