Производные вектора, заданного в подвижном базисе

Если вектор 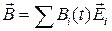, заданный в подвижном базисе, перезаписан в неподвижный базис, то абсолютная производная этого вектора  в неподвижном базисе имеет вид:

Доказательство:

Покажем сначала, что

Вектор  называют абсолютной производной вектор а 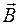 в подвижном базисе, а вектор  называют относительной производной этого вектора в подвижном базисе. Связь между ними, таким образом, имеет вид:

В частности, если вектор 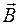 постоянен в подвижном базисе, то 

.

Найдем теперь абсолютную производную вектора 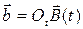, записанного в неподвижном базисе, причем вектор  задан в подвижном базисе:

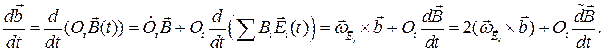
Окончательно:

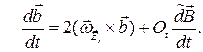
Это соотношение записано в неподвижном базисе.