Траектория какой-либо точки тела есть геометрическое место всех последовательных положений точки при движении тела. Принимаем, что это есть некоторая гладкая кривая линия в 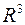 .
.
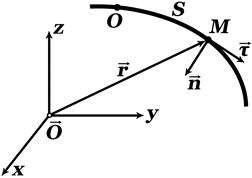
Пусть движение точки тела (далее точки) задано в декартовых координатах:

Выберем на кривой начало отсчета О дуговой координаты s точки М при ее движении как расстояние вдоль кривой от начального положения (точки О) до ее текущего положения М:

 Далее, примем в качестве параметра вместо времени t дуговую координату s:
Далее, примем в качестве параметра вместо времени t дуговую координату s:
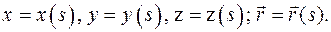
Касательный к траектории вектор 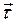 определим следующим образом:
определим следующим образом:
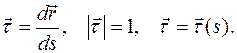
Вектор главной нормали 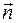 перпендикулярен к вектору
перпендикулярен к вектору 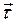

Величина 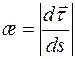 называется кривизной кривой в точке М, а величина
называется кривизной кривой в точке М, а величина 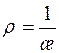 называется радиусом кривизны.
называется радиусом кривизны.
В каждой точке траектории три единичных вектора 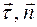 и
и 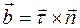 взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.
взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.
Движение точки в естественной форме
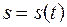
Скорость точки 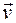 направлена по касательной
направлена по касательной 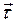 к траектории:
к траектории:

а её проекция на ось 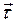 равна:
равна:
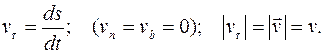
Ускорение точки 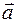 раскладывается по естественному базису так:
раскладывается по естественному базису так:
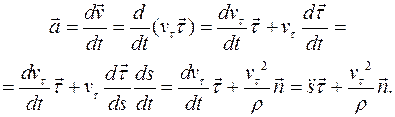
Они называются так: касательное 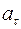 и нормальное
и нормальное 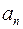 ускорения. Окончательно:
ускорения. Окончательно:
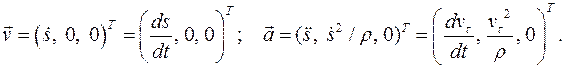
Если траектория точки есть окружность с радиусом R, то кривизна окружности равна, по определению, радиусу окружности, и поэтому нормальное ускорение точки есть
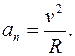
 2020-05-12
2020-05-12 126
126








