Процесс броуновского движения

Пусть частица ξ(t) движется по сетке с шагом и ее положение фиксируется в моменты , причем переходы осуществляются независимыми скачками с вероятностью 1/2 на или на (- ). Пусть ξ(0)=0.

1. За время t совершается шагов: , величины независимы, 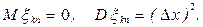Отсюда

2. 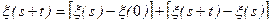- сумма независимых случайных величин, за счет стационарности вторая из них не зависит от s. Тогда

Таким свойством обладает только линейная функция, поэтому . Постоянная σ² называется коэффициентом диффузии. Сравнивая два выражения для дисперсии 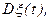получаем, что

3. Перейдем к пределу при и фиксированном t. Понятно, что это нужно делать так, чтобы дисперсия оставалась постоянной, и должны стремиться к нулю согласованно:

Более того, для любого s

Определение. Процесс броуновского движения – это семейство случайных величин таких, что при всех

и приращения на любых непересекающихся интервалах независимы.

Такое определение не обеспечивает непрерывности траекторий процесса. Обычно это условие добавляют специально. При этом траектории оказываются непрерывными нигде не дифференцируемыми функциями.

Контрольные вопросы