Комплексное сопротивление

Отношение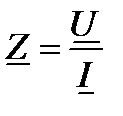

называется комплексным сопротивлением.

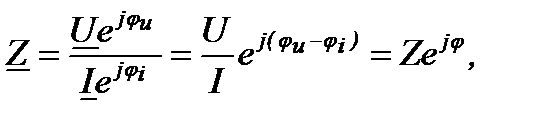
Вычисление x_L   и   x_C

Вычислить x_L. L=25,4 мГ н, f = 50 Гц.

Ом

С=636 мкФ, f =50 Гц.

5.  Вычислить Z при последовательном соединении R, X_L, X_C.

5.1 Вычислить  ветви (рис.4).

R= 160 Ом, x_L= 10 Ом, x_C= 130 Ом.

Переход к показательной форме:

.

Знак минус перед    соответствует знаку минус перед мнимой частью в алгебраической форме числа  (_ указывает на емкостный характер сопротивления цепи).

5.2 Вычислить комплексное сопротивление ветви с резистором (рис.5). R= 2 Ом.

Исходим из формулы

Так как ветвь содержит только R, то X_L=0 и  X_C=0. Следовательно,

5.3 Вычислить  ветви  с конденсатором (рис.6).

Задано  x_C= 5 Ом.

Так как R = 0, x_L = 0, то комплексное сопротивление в алгебраической форме:

В показательной форме:

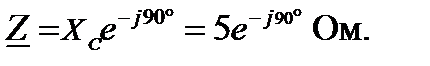
5.4 Вычислить ветви  с идеальной индуктивностью (рис.7). Задано x_L= 8 Ом.

Так как R=0  и x_C= 0, то комплексное сопротивление в алгебраической форме:

В показательной форме:

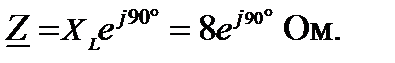
Сложение и вычитание комплексных величин

Сложение и вычитание комплексных чисел проводится в алгебраической форме. Если числа заданы в показательной форме, то их следует перевести в алгебраическую форму.

Например, требуется вычислить ток  (рис.8). Ток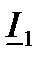и  и   известны:

По первому закону Кирхгофа:

Выразим токи в алгебраической форме: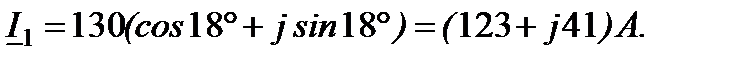

Модуль (действующее значение) и начальная фаза тока :

 

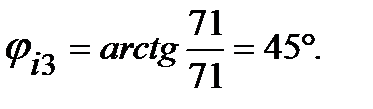
Умножение и деление комплексных величин

 

Умножение и деление проще выполнять, если комплексные числа выразить в показательной форме.

Например, требуется вычислить ток в цепи с активно-индуктивным сопротивлением (рис.9).

Начальная фаза напряжения не задана, следовательно, принимается

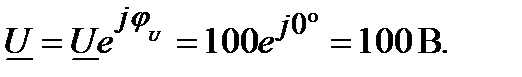
Сопротивление  выразим в показательной форме.

Модуль и аргумент :

Как видно из формулы при делении комплексных чисел их аргументы вычитаются с учётом их знаков. При умножении аргументы складываются. Например,