Длина вектора. Расстояние между двумя точками

Длина вектора

Пусть  – произвольный вектор. Длина вектора  вычисляется по формуле:

 

.

 

Расстояние между двумя точками

Пусть  и  – произвольные точки пространства. Расстояние между точками  и  вычисляется по формуле:

 

.

 

Направляющие косинусы вектора

Направление вектора в пространстве можно задать углами ,  и , которые составляет данный вектор с осями координат. Косинусы этих углов: ,  и  называются направляющими косинусами вектора.

 

 

Рис. 23

Пусть  – произвольный вектор. Согласно формуле проекции вектора на ось будем иметь

 

,

 

,

 

.

 

Отсюда получим значения направляющих косинусов:

 

или

,

 

,

 

.

Из полученных равенств вытекает следующее тождество

 

.

 

Полученное тождество означает, что среди углов ,  и  независимыми являются только два, а третий определяется из тождества (с точностью до знака).

 

Скалярное произведение двух векторов

Определение скалярного произведения

Определение 19. Скалярным произведением векторов 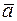 и  называется число, равное произведению их длин на косинус угла между ними и обозначается :

 

.

 

Если известны скалярное произведение векторов 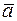,  и их длины , , то угол между векторами (косинус угла между векторами) вычисляют по формуле

 

.

 

Если известны координаты векторов:

 

,   ,

 

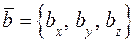то скалярное произведение вычисляется по формуле

 

,

 

а косинус угла – по формуле

 

.

 

 

Свойства скалярного произведения

Свойство 1.  – закон коммутативности.

Свойство 2.  – закон ассоциативности.

Свойство 3.  – закон дистрибутивности.

Свойство 4. ; для того чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.

Свойство 5. ; скалярный квадрат вектора равен квадрату его длины.

 

Векторное произведение двух векторов