Распределительного склада

Рассмотрим задачу, приведенную в задании 2.3. Исходные данные для примера и результаты расчетов представлены на рис. П 2.1, где

Рис. П 2.1. Расчеты задания в MS Excel

1 расчет взвешенного расстояния от пункта до распределительного склада . P₁ в ячейке E2 вычисляется = D2*(($B$9-B2)^2+($B$10-C2)^2)^(1/2), значения нижних ячеек можно получить копированием этой ячейки.

2 В ячейке E8 вычисляется сумма вышестоящих ячеек, т.е. =СУММ(E2:E7).

3 В надстройке «Поиск решения» устанавливаем целевую ячейку $E$8 в «минимальное значение», «изменяя ячейки» $B$9:$B$10 (координаты распределительного склада).

Результаты расчетов приводятся на рис П 2.1, где также приводится диаграмма расположения пунктов и распределительного склада (расположение распределительного склада (треугольник) внесено вручную после определения его координат.

Приложение 3 Решение задачи определения числа

И координат распределительных складов

Рассмотрим задачу, приведенную в задании 2.6. Исходные данные для примера и результаты расчетов представлены на рис. П 3.1.

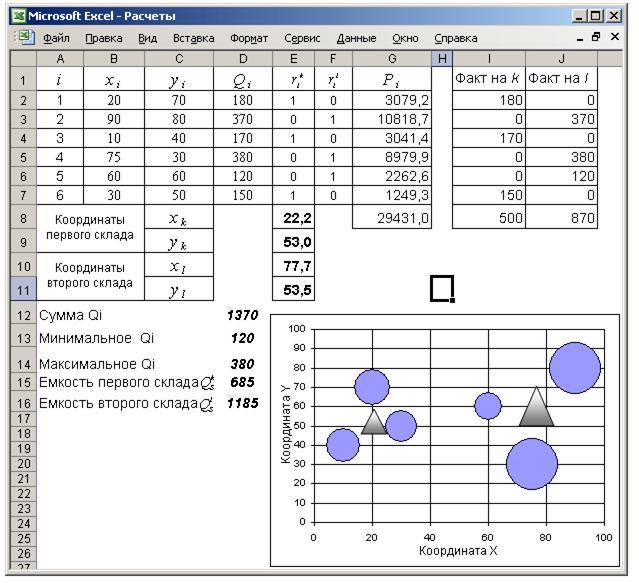
Рис. П 3.1. Расчеты задания 2.6 в MS Excel

Формулы расчета основных ячеек рабочего листа приведены в таблице П 3.1, а параметры окна «Поиск решения» на рис. П 3.2. Дополнительными параметрами для «Поиска решения» является условие неотрицательности переменных (т.к. координаты всех пунктов положительны).

Таблица П 3.1 – Расчетные формулы ячеек

Адрес ячейки	Расчетная формула
F2	=1-E2
G3	=D2(E2(($E$8-B2)^2+($E$9-C2)^2)^(1/2)+F2*(($E$10-B2)^2+($E$11-C2)^2)^(1/2))
I2	=$D2*E2
J2	=$D2*F2
G8	=СУММ(G2:G7)
I8	=СУММ(I2:I7)
J8	=СУММ(J2:J7)
D12	=СУММ(D2:D7)
D13	=МИН(D2:D7)
D14	=МАКС(D2:D7)
D15	=D12/2
D16	=D15+D13+D14