Самым простейшим из методов уточнения корней является метод половинного деления, или метод дихотомии, предназначенный для нахождения корней уравнений, представленных в виде f(x)=0.
Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0
(рис. 2), тогда на отрезке имеется хотя бы один корень.
Возьмем середину отрезка с=(a+b)/2. Если f(a)×f(с)  0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b. Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. (вот вам и цикл) до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (вот и управляющее работой цикла условие) (b-a)<
0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b. Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. (вот вам и цикл) до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (вот и управляющее работой цикла условие) (b-a)<  (или выполнятся другие вышеупомянутые критерии).
(или выполнятся другие вышеупомянутые критерии).

Рис. 2. Метод деления отрезка пополам
Т.к. каждое очередное вычисление f(c) сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешности  количество вычислений n определяется условием (b-a)/2n<
количество вычислений n определяется условием (b-a)/2n<  , или
, или
n~log2((b-a)/  ). Например, при исходном единичном интервале и точности порядка 6 знаков (
). Например, при исходном единичном интервале и точности порядка 6 знаков ( ~ 10-6) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.
~ 10-6) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.
С точки зрения машинной реализации (рис.3) этот метод наиболее прост и используется во многих стандартных программных средствах, хотя существуют и другие более эффективные по затратам времени методы.

Рис.3. Блок-схема метода половинного деления
4. Оснащение: микрокалькуляторы, линейка, карандаш
5. Задания:
1, 3. Отделить корни графически.
2. Отделить корни аналитически и уточнить один из них методом половинного деления.
Индивидуальные задания:
| №1 | 1)  ;
2) ;
2)  ;
3) ;
3) 
| №9 | 1)  ;
2) ;
2)  ;
3) ;
3) 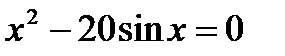 . .
|
| №2 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| №10 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| №3 | 1)  ;
2) ;
2)  ;
3) ;
3)  ; ;
| №11 | 1) 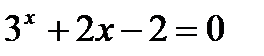 ;
2) ;
2)  ;
3) ;
3)  ; ;
|
| №4 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| №12 | 1)  ;
2) ;
2)  ;
3) ;
3) 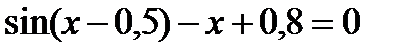 . .
|
| №5 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| №13 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| №6 | 1)  ;
2) ;
2)  ;
3) ;
3)  ; ;
| №14 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| №7 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| №15 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| №8 | 1)  ;
2) ;
2)  ;
3) ;
3) 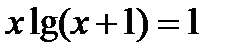 . .
| №16 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
6. Порядок выполнения работы:
Задание 2.
- Обозначить левую часть уравнения за
 и найти первую производную.
и найти первую производную. - Найти корни производной.
- Составить таблицу знаков функции
 , полагая х равным
, полагая х равным
а) корням производной или близким к ним;
б) граничным значениям (исходя из области допустимых значений неизвестного).
| x | 
| Корень | 
|
знак 
|
Если происходит смена знака функции, то уравнение имеет действительный корень.
- Для завершения операции отделения корней следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Составить новую таблицу знаков функции
 .
. - Выбрать промежутки, в которых заключены корни.
- Уточнить один корень до
 методом половинного деления при помощи Microsoft Excel и составить таблицу вида:
методом половинного деления при помощи Microsoft Excel и составить таблицу вида:
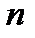
| 
| 
| 
| 
|
| 0 1 2 3 . . . |
Задание 1,3:
1. Переписать уравнение в виде  .
.
2. Построить графики функции  и
и  .
.
3. Корень уравнения – абсцисса точки пересечения графиков.
4. Выбрать промежутки, в которых заключены корни.
7. Контрольные вопросы:
- Виды уравнений.
- Что является решением уравнения?
- Что значит отделить корень?
- Методы отделения корней уравнения (описать).
- Метод половинного деления (описать и составить блок-схему алгоритма метода)
6. Оценка погрешности приближения в данном методе (формула).
8. Требования к отчету: Отчет должен быть оформлен в соответствии с требованиями ЕСКД. Содержать цель, задание, таблицы, выводы.
9. Литература:
1. В.Н.Исаков, «Элементы численных методов».- М., АКАДЕМА,2003
2. А.А.Гусак. «Справочник по математике».- Минск, ТетраСименс,1999
 2020-05-11
2020-05-11 326
326








