Правила построения диаграммы

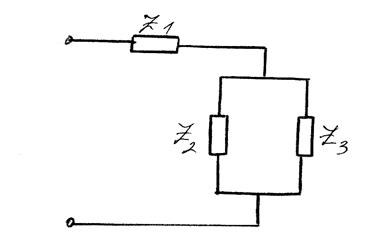
1. На оси X откладываем действительную часть, на оси Y – мнимую часть.

2. Строим вектора напряжений: на участке Z₁, на разветвлении и подаваемое напряжение.

3. Строим вектора токов в параллельных ветвях и в неразветвленной части цепи.

4. Если задача решена правильно, то должны выполняться равенства:

 

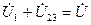
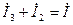
Порядок выполнения работы

1. Записать тему, цель, исходные данные своего варианта.

2. Записать сопротивления каждого участка в комплексной форме.

3. Определить комплекс сопротивления разветвления.

4. Определить комплекс полного сопротивления.

5. Найти комплекс тока в неразветвленной части цепи.

6. Определить комплексы напряжений на участке z₁ и на разветвлении.

7. Найти комплексы токов в параллельных ветвях.

8. Построить диаграмму на комплексной плоскости в масштабе.

9. Сделать вывод.

10. Сдать работу преподавателю.

 

Система оценки – пятибальная

 

Задание на расчет

№ варианта	U,B	Z1		Z2		Z3
		R1, Ом	X1, Ом	R2, Ом	X2, Ом	R3, Ом	X3, Ом
1	220	3	WL1=4	64	WL2=48	6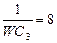
2	380	4	WL1=3	16		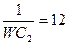40	WL3=30
3	220	8		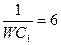12		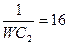4	WL3=3
4	380	6	WL1=8	40	WL2=30	24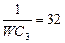
5	380	16		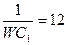3	WL2=4	8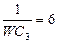
6	220	12		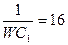15		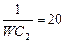30	WL3=40
7	220	4	WL1=3	48	WL2=64	40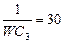
8	380	8		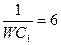24		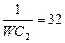20	WL3=15
9	380	24	WL1=32	8		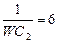12	WL3=16
10	220	12		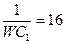20	WL2=15	32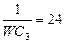
11	380	4	WL1=6	60	WL2=50	6	WL3=8
12	380	5		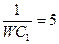17	WL2=12	40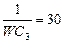
13	380	9		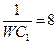13	WL2=16	6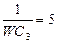
14	220	7	WL1=10	42		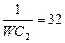24	WL3=30
15	220	17	WL1=14	4		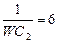10	WL3=6
16	220	13		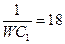16		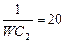32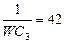

 

Контрольные вопросы

 

1. Что такое комплекс сопротивления, комплекс проводимости?

2. Записать и сформулировать закон Ома в комплексной форме.

3. Какой порядок расчета электрической цепи при смешанном соединении элементов символическим методом?

4. Правила построения диаграммы на комплексной плоскости.

 

 

Список использованной литературы

 

1 Евдокимов Ф.Е. «Теоретические основы электротехники», Москва.

 «Высшая школа», 1999г.

 

 

Практическое занятие 14