2020-05-12
170
Момент равнодействующей сходящейся системы сил относительно любой точки на плоскости равен алгебраической сумме моментов составляющих сил относительно той же точки.
Рассмотрим плоскую сходящуюся систему сил, в точке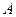 
(рис. 28а).
24
a) б) в)
рис.28
Заменим эту систему сил равнодействующей, приложенной в той же точке (рис. 28б). Определим момент этой равнодействующей относительно точки 
, лежащей на оси 
(рис. 28в). Разложим равнодействующую на составляющие и , каждая из которых будет определяться: 
, 
. Определяя момент этих проекций относительно точки (рис. 20в), очевидно, что 
, т.к. 
пересекает точку . Тогда 
. Аналогично рассматривая каждую из сил (рис. 28а), получим, что момент каждой из них относительно точки будет определяться моментом проекции этих сил на ось , относительно точки , т.е. 
, 
, 
. Учитывая, что 
получаем:
(7)
