2020-05-12
143
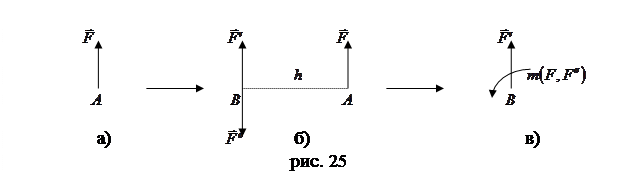
Пусть на тело действует система из «n» сил, лежащих в одной плоскости. Мы умеем их складывать, если они пересекаются в одной точке или они параллельны. Однако, если эти силы в плоскости расположены произвольно, то появляется необходимость привести эти силы к какому то центру. Покажем эту процедуру приведения силы к данному центру на примере одной силы. Теорема. Любая данная сила эквивалентна такой же по модулю и направлению сил, но приложенной в другой точке тела и некоторой паре.
 |
Дана сила,
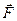приложенная в точке 
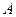(рис. 25а). Требуется привести эту силу к произвольно выбранному центру 
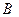причем так, чтобы состояние тела при этом не изменилось. Прикладываем в точке 
две прямопротивоположные силы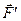 
и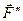 
равные по модулю силе 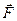(рис. 25б). Тогда силы 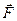и 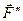образуют пару. Следовательно, данную силу 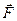можно заменить равной ей силой 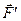, приложенной в любой точке тела и парой 
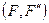, с моментом 
, что и требовалось доказать (рис. 25в).
Из доказанной теоремы получаем, что данную силу можно переносить параллельно самой себе в любую точку тела с присоединением соответствующей пары. Поэтому пару 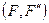называют присоединенной. Алгебраический момент присоединенной пары равен 
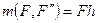. С другой стороны произведение 
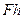представляет собой момент силы 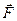, относительно нового центра приведения 
: 
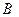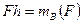. Следовательно, 
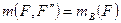момент присоединенной пары 
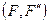равен моменту силы 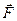, приложенной в старом центре 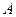, относительно нового центра .
|
|
|
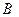22
