2020-05-12
407
Пусть движение задано в векторной форме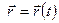 
. Точка М движется по некоторой криволинейной траектории 
и ее положение определяется вектором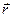 
. Пусть в момент времени 
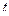положение точки 
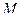определяется вектором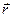 
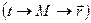. В момент времени 
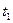, отличающийся от первоначального на бесконечно малый промежуток времени 
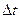, точка занимает положение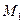 
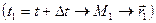. Таким образом, в каждый момент времени конец вектора будет находиться точки 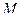. Геометрическое место концов этих векторов, или, линия, описываемая в пространстве концом вектора, начало которого находится в данной неподвижной точке называется годографом этого вектора. Очевидно, что годографом радиуса – вектора 
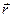движущейся точки 
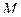является траектория 
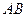этой точки.
 |
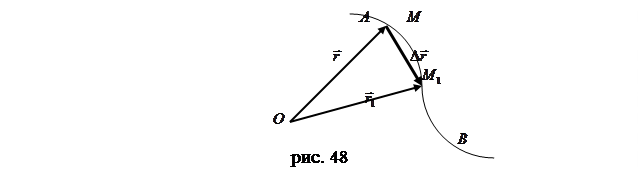Соединим точк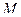и 
и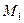 
прямой (рис. 48), тогда, очевидно, можно записать векторное равенство 
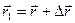или 
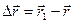, где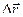 
- есть изменение (приращение) данного вектора 
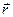за время 
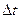. Разделив это приращение на промежуток времени 
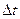, получим новый вектор, имеющий тоже направление, но другую величину. Этот вектор 
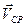называется средней скоростью точки за время 
.
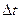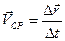(23)
Средняя скорость криволинейного движения - это скорость такого равномерного движения, при которой точка, двигаясь по хорде равномерно попадает на траекторию в тоже положение, которое она занимает через данный промежуток времени, двигаясь по траектории неравномерно.
Будем теперь приближать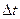 
к нулю. При этом точка 
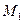будет при этом приближаться к точке 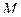. В пределе направление вектора 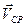(также как и 
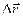) совпадает с направлением касательной к траектории в точке 
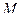, а модуль его равен 
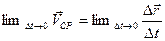. Предел средней скорост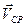и при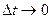 
называется скоростью движущейся точки в момент времени 
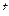или истинной скоростью точки.
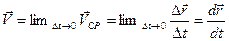(24)
42
Вектор истинной скорости равен векторной производной от радиуса вектора, определяющего положение точки, по времени. Вектор истинной скорости имеет направление касательной к траектории в данном положении точки.
Определим модуль вектора истинной скорости. Введем обозначение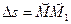 
- дуга траектории, тогда 
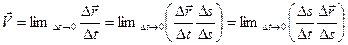. Учитывая, что предел производной равен произведению пределов 
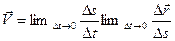. Мы определяем модуль, т.е. переходим от векторных величин к скалярным 
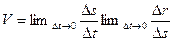. Учитывая, что 
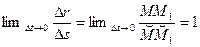, получаем 
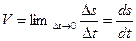, где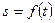 
.
Таким образом, модуль вектора скорости равен производной от дуговой координаты движущейся точки по времени.
Если производная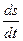 
положительна, то с ростом времени возрастает и 
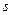, т.е. точка движется по траектории в положительном направлении и наоборот. Если модуль 
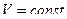, то получаем случай равномерного криволинейного движения. В этом случае величина 
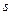является линейной функцией времени, т.е. 
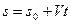, где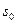 
- начальное значение дуговой координаты при 
.
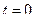Для случая прямолинейного движения было получено, что ускорение точки выражается производной от скорости по времени (21). В случае криволинейного движения эта производная, очевидно, не может полностью характеризовать изменение скорости по времени, так как здесь скорость меняется не только по модулю, но и по направлению рис. 49. Для случая криволинейного движения, вектор ускорения строят следующим образом. Пусть в момент времени 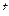, движущаяся точка занимает на траектории положение 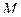и имеет скорость 
.
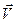43
Через малый промежуток времени 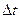, т.е. в момент 
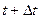, эта точка занимает положение 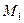и имеет скорость 
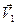. Перенесем начало вектора 
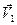в точку 
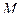, соединим конец вектора 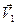и 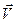, а затем достроим полученный треугольник до параллелограмма. Тогда вектор 
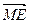представляет собой изменение скорости за время : 
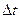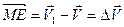. Построим теперь новый вектор 
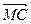, равный отношению изменения скорости 
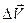к соответствующему промежутку времени 
. 
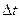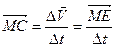. Этот вектор называется средним ускорением точки за время 
:
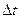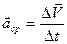(25)
Предел, к которому стремится среднее ускорение при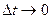 
, называется ускорением точки в данный момент времени
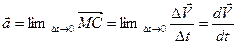(26)
