Связь между различными способами задания движения

    В этом параграфе показано, как можно сделать переход от одного способа задания движения точки к другому.

а) Переход от координатного способа задания движения к векторному. 

Эту связь легко получить, если ввести единичные векторы (орты) осей 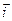, , 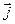 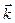(рис. 43). Тогда учитывая, что проекции вектора  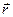на оси  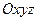равны координатам точки 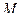, т.е. 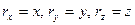, получаем:

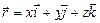                                                                                              (16)

По зависимости (16), можно сделать переход от координатного способа задания движения к векторному, и наоборот 

б) Переход от координатного способа задания движения к естественному. 

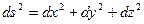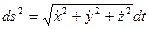    Допустим, что движение задано в виде уравнений (14). Известно, что  или , где 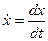, , 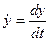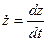. Отсюда получаем:  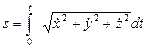                                                                            (17)