2020-05-12
556
Рассмотрим два последовательных положения 
и 
, которые занимает тело в моменты времени 
и 
(рис. 61). Тело из положения в положение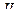 
можно перенести следующим образом. Перенесем сначала тело поступательно. При этом отрезок 
переместится параллельно самому себе в положение 
, а затем повернем тело вокруг точки (полюса)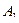 
на угол 
, до совпадения точек 
и 
.
55
Следовательно, любое плоское движение можно представить как сумму поступательного вместе с выбранным полюсом и вращательного, относительно данного полюса.
| Определение скоростей точек плоской фигуры. |
Рассмотрим методы, с помощью которых можно определить скорости точек тела, совершающего плоское движение.
1. Метод полюса. Этот метод основывается на полученном разложении плоского движения на поступательное и вращательное. Скорость любой точки плоской фигуры можно представить в виде двух составляющих: поступательная, со скоростью равной скорости произвольно выбранной точки – полюса, и вращательной, вокруг этого полюса.
|
|
|
Рассмотрим плоское тело (рис. 62). Уравнения движения имеют вид: 
, 
, 
.
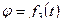Определяем из этих уравнений скорость точки 
(как при координатном способе задания)
, 
, 
.
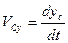Таким образом, скорость точки - величина известная. Принимаем эту точку за полюс и определим скорость произвольной точки 
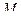тела.
56
Скорость 
будет складываться из поступательной составляющей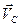 
, при движении вместе с точкой и вращательной 
, при вращении точки 
относительно точки . Скорость точки перенесем в точку параллельно самой себе, т.к. при поступательном движении скорости всех точек равны как по величине, так и по направлению. Скорость определится по зависимости (50) 
и направлен этот вектор перпендикулярно радиусу 
по направлению вращения 
. Итоговый вектор будет направлен по диагонали параллелограмма, построенного на векторах 
и 
, а его модуль определиться зависимостью:
, 
(55)
2. Теорема о проекциях скоростей двух точек тела.
Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой.
Рассмотрим две точки тела 
и 
(рис. 63). Принимая точку за полюс, определим направление 
по зависимости (55): 
. Проектируем это векторное равенство на линию и учитывая, что 
перпендикулярно , получаем:
(56)
3. Мгновенный центр скоростей.
Мгновенным центром скоростей (МЦС) называется точка твердого тела, скорость которой в данный момент времени равна нулю.
|
|
|
Покажем, что если тело движется не поступательно, то такая точка в каждый момент времени существует и при том единственная. Пусть в момент времени точки и тела, лежащие в сечении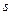 
, имеют скорости 
и , не параллельные друг другу (рис. 64). Тогда точка 
, лежащая на пересечении перпендикуляров к векторам и 
, и будет МЦС, т.к.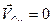 
.
Действительно, если допустить, что 
, то по теореме (56), вектор 
должен быть одновременно перпендикулярен 
и 
, что
57
невозможно. Из этой же теоремы видно, что никакая другая точка сечения 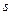в этот момент времени не может иметь скорость, равную нулю.
Применяя метод полюса - полюс, определим скорость точки (55): 
, т.к. 
, 
(57)
Аналогичный результат можно получить для любой другой точки тела. Следовательно, скорость любой точки тела, равна ее вращательной скорости относительно МЦС.
, 
, 
, т.е. скорости точек тела пропорциональны их расстояниям до МЦС.
Из рассмотренных трех способов определения скоростей точек плоской фигуры видно, что предпочтительным является МЦС, т.к. здесь скорость сразу определяется как по модулю, так и по направлению одним вектором. Однако этот способ можно применять, если нам известен или мы можем определить для тела положение МЦС.
Определение положения МЦС.
а) Если нам известно для данного положения тела направления скоростей двух точек тела, то МЦС будет точкой пересечения перпендикуляров к этим векторам скоростей (рис. 65).
б) Скорости двух точек тела антипараллельны (рис. 65а). В этом случае перпендикуляр к скоростям будет общим, т.е. МЦС находится, где-то на этом перпендикуляре. Чтобы определить положение МЦС надо соединить концы векторов скоростей. Точка пересечения этой линии с перпендикуляром будет искомым МЦС. При таком случае МЦС находится между этими двумя точками.
58
в) Скорости двух точек тела параллельны, но не равны по величине (рис. 65б). Процедура получения МЦС аналогична описанной в пункте б).
г) Скорости двух точек равны как по величине, так и по направлению (рис. 65в). Получаем случай мгновенно поступательного движения, при котором скорости всех точек тела равны. Следовательно, угловая скорость тела в данном положении равна нулю: 
.
д) Определим МЦС для колеса, катящегося без скольжения по неподвижной поверхности (рис. 65г). Так как движение происходит без скольжения, то в точке контакта колеса с поверхностью скорость будет одинакова и равна нулю, т.к. поверхность неподвижна. Следовательно, точка контакта колеса с неподвижной поверхностью будет являться МЦС.
