В-сплайны первого порядка

1). Результаты наблюдений за изменением входной и выходной переменной отображают на графике (рис. 2).

 

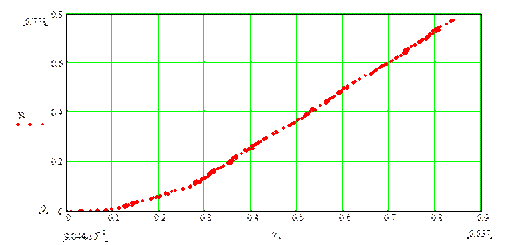
Рис.2. Графическое изображение результатов измерений

2). Осуществляют анализ полученного графика, в результате которого определяют диапазон изменения входной переменной, интервал 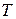 непрерывности В-сплайна 1-го порядка (в пределах которого экспериментальные точки на графике достаточно хорошо располагаются на отрезках прямых линий) и количество  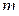таких интервалов.

3). Функциональную зависимость результирующей переменной 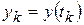 от влияющего фактора

; ; ; ;

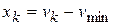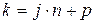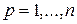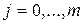(1)

описывают В-сплайнами 1-го порядка:

,

(2)

где: 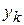 - наблюдаемое (измеряемое) значение результирующей переменной в момент времени ;

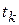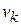 - наблюдаемое (измеряемое) значение входной переменной в момент времени ;

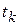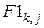 - известные финитные функции переменной  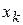(В-сплайны 1-го порядка):

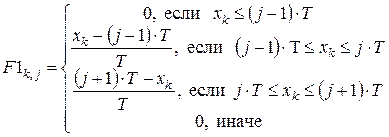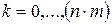; ;    (3)

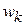 - неизвестное возмущающее воздействие (погрешность математической модели), которое является величиной второго порядка малости по сравнению с первым слагаемым правой части равенства (2);

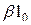 , …,  - неизвестные параметры, подлежащие определению на этапе параметрической идентификации математической модели анализируемого процесса, объединенные в вектор параметров

;

(4)

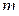- число интервалов непрерывности сплайнов ;

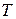- число измерений внутри одного интервала .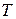

 

В-сплайны третьего порядка

При описании модели анализируемого процесса В-сплайнами 3-го порядка

; ;

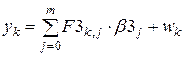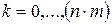(5)

 используют финитную функцию:

(6)

где 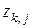 - вспомогательная функция

.

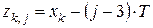(7)

Интерференция финитных функций 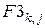 приведена на рис. 3:

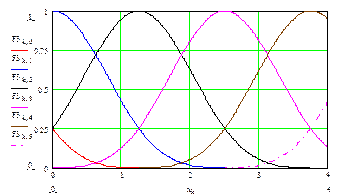
Рис. 3.

АЛГОРИТМ ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ

МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Постановка задачи идентификации параметров