2020-05-11
206
Задача №6.
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю: 5000000рублей
| Часы в неделю | Единицы товара в неделю | Оплата за 1 час | Полная оплата | |
| 1 завод | x2 | 3x | 500 | 500 
|
| 2 завод | y2 | 4y | 500 | 500 
|
Составим функцию количества единиц товара:
∑(x,y) = 3x+4y→наиб
Заметим, что 500 
+500 
5000000, т.е. x 
где y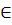 
∑(y) =3 
+4y→наиб
Возьмём производную этой функции
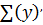= 3 
+4 = 
Найдём нули производной: =0
=0
9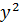 
=16(10000- )
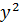25 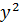=1600000
y=80
Функция принимает своё наибольшее значение при y=80 (точка максимума).
x 
= 
=60
Найдём количество единиц товара: 3 
+4 
80 = 180+320 = 500
