Задача №12.
Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
| Вид тары | Себестоимость,1 ц. | Отпускная цена,1 ц. |
| стеклянная | 1500 руб. | 2100 руб. |
| жестяная | 1100 руб. | 1750 руб. |
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
Решение
Пусть x центнеров выпускает фабрика в стеклянной таре, а y центнеров – в жестяной. Тогда по условию имеем: x 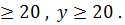
Составим функцию прибыли:
∑(x,y) = 600x+650y→наиб
Пусть производственная возможность равна 1, тогда 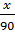 +
+ 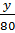 = 1
= 1
80x + 90y = 7200
x = 90 – 1,125y
∑(y) = 600(90 – 1,125y)+650y→наиб
∑(y) = 54000 - 25y→наиб
Возьмём производную этой функции
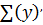 =
= 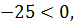
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=20. Тогда x = 90-1,12 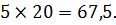
При этом максимальная прибыль будет 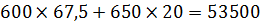 рублей.
рублей.
Ответ: 53500 рублей.
Нестандартные задачи
Задача №1.
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние?
Решение:
| Скорость | Время | Расстояние | |
| 1 велосипедист | 40 | t | 40t |
| 2 велосипедист | 30 | t | 30t |
Составим функцию квадрата расстояния между велосипедистами:
∑(t) = 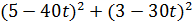 →наим, где t
→наим, где t 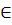
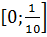
∑(t) = 25-400t+1600 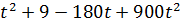 →наим
→наим
∑(t) = 2500 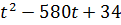 →наим
→наим
Возьмём производную этой функции
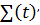 = 5000t-580
= 5000t-580
Найдём нули производной: 5000t-580=0
t = 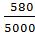 =
= 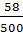 =
= 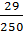
Функция принимает своё наименьшее значение при t= 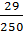 ч = 60
ч = 60 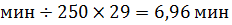 (точка минимума).
(точка минимума).
Найдём расстояние между велосипедистами: 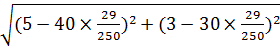 =
= 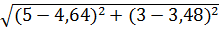 =
= 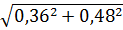 =
= 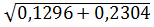 =
= 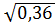 = 0,6
= 0,6
 2020-05-11
2020-05-11 1382
1382








