РАБОЧАЯ ТЕТРАДЬ
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Баранова Е.С.
Санкт-Петербург
2006
Задача 1
Изобразить число  на комплексной плоскости, найти
на комплексной плоскости, найти
его модуль и аргумент и записать в тригонометрической и экспоненциальной формах.
Справочный материал
Комплексным числом  называется выражение вида
называется выражение вида  , где
, где  и
и  — любые действительные числа,
— любые действительные числа, 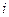 — мнимая единица, удовлетворяющая условию
— мнимая единица, удовлетворяющая условию  .
.
Запись  называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Действительные числа  и
и  называются соответственно действительной (или вещественной) и мнимой частью комплексного числа
называются соответственно действительной (или вещественной) и мнимой частью комплексного числа  и обозначаются
и обозначаются
 ,
,  .
.
Комплексное число  называется сопряженным числу
называется сопряженным числу  .
.
Комплексное число  можно изображать на плоскости
можно изображать на плоскости 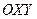 вектором
вектором 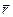 с началом в точке
с началом в точке  и концом в точке
и концом в точке  . Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной (или вещественной) осью, а ось ординат — мнимой (рис. 1).
. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной (или вещественной) осью, а ось ординат — мнимой (рис. 1).

Рис. 1.
Длина вектора  называется модулем комплексного числа
называется модулем комплексного числа  и обозначается
и обозначается  . Величина угла между положительным направлением действительной оси и вектором
. Величина угла между положительным направлением действительной оси и вектором 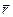 называется аргументом числа
называется аргументом числа  :
:  . Положительным направлением изменения угла
. Положительным направлением изменения угла  считается направление против часовой стрелки. Модуль и аргумент комплексного числа
считается направление против часовой стрелки. Модуль и аргумент комплексного числа  определяются из формул:
определяются из формул:
 ,
,  .
.
При нахождении аргумента следует учитывать, что для каждого числа  его аргумент имеет бесконечное множество значений, отличающихся друг от друга на число, кратное
его аргумент имеет бесконечное множество значений, отличающихся друг от друга на число, кратное 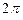 (аргумент числа
(аргумент числа  не определён, а его модуль равен нулю). В качестве главного значения аргумента обычно выбирают значение
не определён, а его модуль равен нулю). В качестве главного значения аргумента обычно выбирают значение  из промежутка
из промежутка  . Всё множество значений аргумента обозначают
. Всё множество значений аргумента обозначают 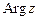 . Таким образом,
. Таким образом,
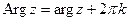 (
( ).
).
Если  ,то из формулы
,то из формулы  получаем
получаем
| для внутренних точек I и IV четвертей, то есть при  , ,
|
для внутренних точек II четверти, то есть при  , ,  , ,
| |
для внутренних точек III четверти,
то есть  , ,  . .
|
Выделим четыре частных случая. Если z:
a) действительное положительное число, то  ;
;
б) действительное отрицательное число, то 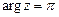 ;
;
в) чисто мнимое с положительной мнимой частью, то 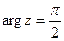 ;
;
г) чисто мнимое с отрицательной мнимой частью, то  .
.
Любое комплексное число  можно представить в тригонометрической форме
можно представить в тригонометрической форме
 ,
,
 С помощью формулы Эйлера
С помощью формулы Эйлера

можно перейти от тригонометрической формы записи комплексного числа к экспоненциальной (показательной).
 .
.
Решение задачи
Число  изобразим на комплексной плоскости точкой с координатами
изобразим на комплексной плоскости точкой с координатами  (рис. 2).
(рис. 2).
Найдем модуль заданного числа:
 .
.
Так как точка  лежит во второй четверти, то
лежит во второй четверти, то
 .
.

Рис. 2.
Тригонометрическая форма имеет вид
 ,
,
а экспоненциальная
 .
.
Задача 2
Найти а)  , б)
, б)  .
.
Справочный материал
Для того чтобы разделить одно комплексное число на другое, удобно домножить числитель и знаменатель дроби, полученной при записи действия, на комплексное число, сопряженное знаменателю:

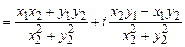 .
.
Решение задачи 2а

 .
.
Решение задачи 2б
Представим  в тригонометрической форме и найдем действительную часть:
в тригонометрической форме и найдем действительную часть:

 .
.
Задача 3
Вычислить  .
.
Решение задачи
Учитывая, что  , и
, и 
 , получаем
, получаем
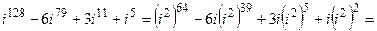
 .
.
Задача 4
Вычислить  .
.
Решение задачи
Представим числа  и
и  в показательной форме:
в показательной форме:
 ;
;
 ,
,
и возведем их в степени:
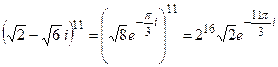 ,
,
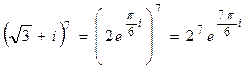 .
.
Тогда
 .
.
Так как
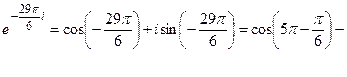
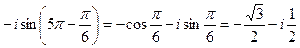 ,
,
получаем
 .
.
Задача 5
Вычислить и изобразить на комплексной плоскости  .
.
Справочный материал
Извлечь корень натуральной степени  из числа z - значит найти такое число
из числа z - значит найти такое число  ,
,  - я степень которого равна z.
- я степень которого равна z.
Если 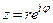 , то
, то

 ,
,  .
.
Все  различных значений
различных значений  имеют один и тот же модуль, равный
имеют один и тот же модуль, равный  . Аргументы значений
. Аргументы значений  и
и  отличаются один от другого на
отличаются один от другого на  . Поэтому точки, соответствующие значениям
. Поэтому точки, соответствующие значениям  , являются вершинами правильного
, являются вершинами правильного  - угольника, вписанного в окружность радиуса
- угольника, вписанного в окружность радиуса  с центром в начале координат.
с центром в начале координат.
Решение задачи
Найдем модуль и аргумент числа  :
:
 ,
,
 .
.
Следовательно,
 .
.
Полагая  , найдем пять различных значений корня:
, найдем пять различных значений корня:

|  , ,
|

|  , ,
|

|  , ,
|
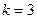
| 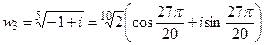 , ,
|

|  . .
|
Изобразим полученные значения на комплексной плоскости (рис. 3).

Рис. 3.
Задача 6
Найти все значения функций:
а)  , б)
, б)  , в)
, в)  .
.
Справочный материал
Пусть даны два множества  и
и 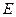 , принадлежащих расширенной комплексной плоскости.
, принадлежащих расширенной комплексной плоскости.
Если каждому числу  из множества
из множества  поставлено в соответствие одно число
поставлено в соответствие одно число  из множества
из множества 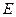 , то говорят, что на множестве
, то говорят, что на множестве  определена однозначная функция комплексной переменной
определена однозначная функция комплексной переменной  , отображающая множество
, отображающая множество  во множество
во множество 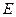 .
.
Множество  всех значений
всех значений  , которые
, которые  принимает на
принимает на 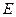 , называется множеством значений функции
, называется множеством значений функции  .
.
Если каждому значению  из множества
из множества  ставится в соответствие несколько значений
ставится в соответствие несколько значений  из множества
из множества 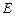 , то функция
, то функция  называется многозначной.
называется многозначной.
Представим каждое из комплексных чисел  и
и  в виде
в виде  ,
,  . Тогда
. Тогда
 .
.
Таким образом, задание функции комплексной переменной  равносильно заданию двух действительных функций
равносильно заданию двух действительных функций  и
и  .
.
Перечислим основные элементарные функции комплексной переменной.
Показательная функция  определяется с помощью равенства
определяется с помощью равенства
 .
.
Показательная функция является периодической с периодом 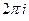 , т. е.
, т. е.  .
.
Тригонометрические функции определяются равенствами
 ,
,  ,
,
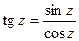 ,
,  .
.
 2020-05-13
2020-05-13 117
117








