Основная теорема о вычетах

Если функция  является аналитической в замкнутой области , ограниченной контуром , за исключением конечного числа  изолированных особых точек , лежащих внутри , то

.

Решение задачи

Конечными особыми точками функции  являются нули ее знаменателя, т. е. точки 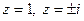. При этом,  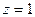- полюс второго порядка, а  и  - полюсы

первого порядка, т. к. .

а) Контур  представляет собой окружность единичного радиуса с центром в точке  (рис. 9). Внутри этой окружности находится только полюс первого порядка .

Рис. 9.

Найдем вычет в этой точке:

.

Тогда .

б) Внутри контура , представляющего собой окружность радиуса 2 с центром в начале координат, находятся точки  - полюс второго порядка, 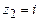 и  - полюсы первого порядка (рис. 10).

Рис. 10.

В пункте (а) был найден вычет в полюсе 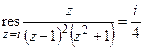.Вычислим вычеты в остальных полюсах:

,

.

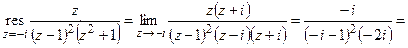
Окончательно получаем .

в) Внутри окружности  нет особых точек (рис. 11), и тогда по теореме Коши .

Рис. 11.

Задача 12

Вычислить несобственные интегралы, используя вычеты

а) , б) .

Справочный материал

Несобственный интеграл I рода

а) Пусть функция  аналитическая в верхней полуплоскости, включая действительную ось, за исключением конечного числа особых точек , лежащих в верхней полуплоскости.

Пусть, кроме того,  при , . Тогда

.

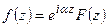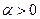б) Пусть функция  имеет вид , где , а  аналитическая в верхней полуплоскости, включая действительную ось, за исключением конечного числа особых точек , лежащих в верхней полуплоскости и . Тогда

.

При нахождении интегралов вида

следует сначала получить значение интеграла , а затем выделить его мнимую и вещественную части.

Решение задачи

а). Введем функцию 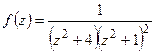. В верхней полуплоскости  имеет один полюс первого порядка в точке  и один полюс второго порядка в точке . Найдем вычеты в этих точках:

.

.

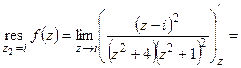
Окончательно, .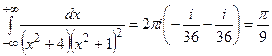

б) Так как подынтегральная функция  четная, то

.

Подынтегральную функцию можно представить в виде , поэтому искомый интеграл

.

Функция  имеет в верхней полуплоскости полюс второго порядка в точке 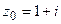. Найдем вычет в :

.

Так как

,

то окончательно получаем

.

 

Вариант 1

1. Изобразить число  на комплексной плоскости, найти
его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) ; б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .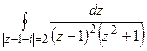

12. Вычислить несобственный интеграл, используя вычеты

.

 

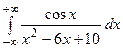Вариант 2

1. Изобразить число 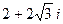 на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости

6. Найти все значения функций: а) 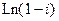, б) .

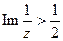7. Нарисовать заданные линии или области: а) , б) , в) .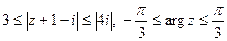

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 3

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .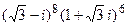

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) ; б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .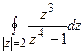

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 4

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

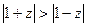7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 5

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) 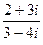, б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) ; б) .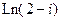

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 6

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .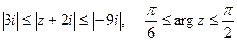

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 7

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) ; в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки 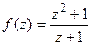 и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 8

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .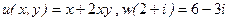

9. Куда отобразится линия при отображении ?

10. Исследовать конечные особые точки 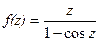 и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 9

1. Изобразить число 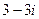 на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части: .

9. Куда отобразится линия при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 10

 

1. Изобразить число 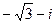 на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл: .

12. Вычислить несобственный интеграл, используя вычеты:

.

Вариант 11

 

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) 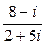, б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 12

 

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 13

 

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия 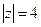при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 14

 

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) , б) .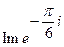

3. Вычислить .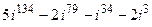

4. Вычислить .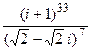

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

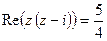7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 15

 

1. Изобразить число  на комплексной плоскости, найти его модуль и аргумент, записать в тригонометрической и экспоненциальной формах.

2. Найти: а) 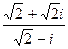, б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) 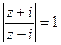, б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

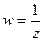10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

 

Вариант 16

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) 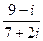, б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) 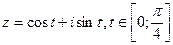, б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия 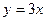 при отображении ?

10. Исследовать конечные особые точки 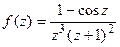 и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 17

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 18

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .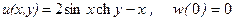

9. Куда отобразится линия  при отображении ?

10. Исследовать особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 19

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

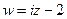10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 20

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия 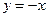 при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 21

 

1. Найти модуль и аргумент числа 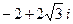, записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .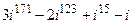

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее мнимой части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 22

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .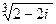

6. Найти все значения функций: а) , б) .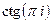

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия  при отображении ?

10. Исследовать конечные особые точки  и найти в них вычеты.

11. Вычислить интеграл .

12. Вычислить несобственный интеграл, используя вычеты

.

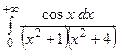Вариант 23

 

1. Найти модуль и аргумент числа , записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости.

2. Найти: а) , б) .

3. Вычислить .

4. Вычислить .

5. Вычислить и изобразить на комплексной плоскости .

6. Найти все значения функций: а) , б) .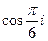

7. Нарисовать заданные линии или области: а) , б) , в) .

8. Восстановить аналитическую функцию по ее вещественной части .

9. Куда отобразится линия 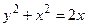 при отображении ?

10. Исследовать конечные особые точки 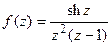 и найти в них вычеты.

11. Вычислить интеграл .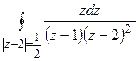

12. Вычислить несобственный интеграл, используя вычеты

.

Вариант 24

 

1. Найти модуль и аргумент числа , записать его в три