Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством6 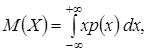 где р (х) — плотность распределения случайной величины Х.
где р (х) — плотность распределения случайной величины Х.
Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством: 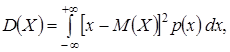
или равносильным равенством 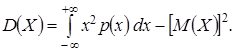 Если все возможные значения Х принадлежат интервалу
Если все возможные значения Х принадлежат интервалу 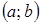 , то
, то 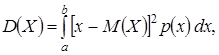 или
или
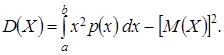 Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины определяется равенством:
Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины определяется равенством: 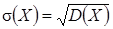 .
.
Равномерный закон распределения
Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке 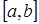 , если ее плотность вероятности р (х) постоянна на этом отрезке и равна нулю вне его, т.е.
, если ее плотность вероятности р (х) постоянна на этом отрезке и равна нулю вне его, т.е.
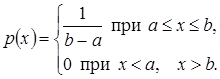
Функция распределения случайной величины Х, распределенной по равномерному закону, есть
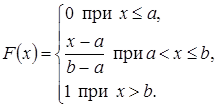
Математическое ожидание 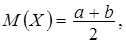 дисперсия
дисперсия 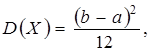 а среднее квадратическое отклонение
а среднее квадратическое отклонение 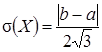 .
.
Экспоненциальный закон распределения
Непрерывная случайная величина Х имеет показательный(экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид
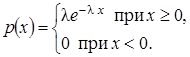
Функция распределения случайной величины, распределенной по показательному закону, равна
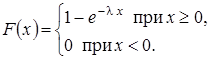
Для случайной величины, распределенной по показательному закону: 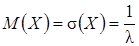 ;
; 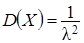 . Вероятность попадания в интервал
. Вероятность попадания в интервал 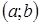 непрерывной случайной величины Х, распределенной по показательному закону:
непрерывной случайной величины Х, распределенной по показательному закону: 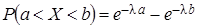 .
.
 2020-05-11
2020-05-11 277
277








