Тема 8 закон больших чисел

Нижеприведенные утверждения и теоремы составляют содержание группы законов, имеющих общее название - закон больших чисел.

Неравенство Маркова. Пусть Х — неотрицательная случайная величина, т.е. 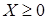. Тогда для любого 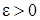: 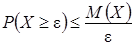, где М (Х) — математическое ожидание Х.

Следствие 1. Так как события  и 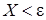 противоположные, то неравенство Маркова можно записать в виде: .

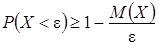Неравенство Чебышева. Для любой случайной величины Х, имеющей конечную дисперсию и любого : .

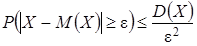Следствие 2. Для любой случайной величины Х с конечной дисперсией и любого : .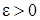

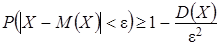Теорема Чебышева. Если  последовательность независимых случайных величин с математическими ожиданиями 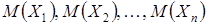 и дисперсиями 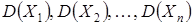, ограниченными одной и той же постоянной 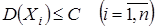, то какова бы ни была постоянная , .

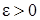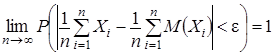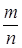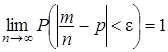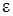Теорема Бернулли. При неограниченном увеличении числа независимых опытов частость появления некоторого события А сходится по вероятности к его вероятности р = Р (А): , где — сколь угодно малое положительное число.

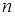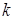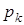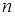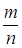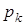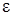Теорема Пуассона. Если производится независимых опытов и вероятность появления события А в -м опыте равна , то при увеличинении частость  события А сходится по вероятности к среднеарифметическому вероятностей : , где — сколь угодно малое положительное число.