Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 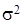 , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид: 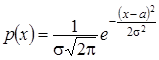 . Кривую нормального закона распределения называют нормальной или гауссовой кривой. Нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный
. Кривую нормального закона распределения называют нормальной или гауссовой кривой. Нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 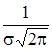 , и две точки перегиба
, и две точки перегиба 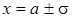 с ординатой
с ординатой 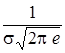 . Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф (х) по формуле:
. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф (х) по формуле: 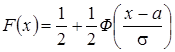 , где
, где 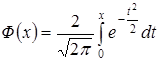 .
.
Вероятность попадания значений нормальной случайной величины Х в интервал 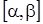 определяется формулой:
определяется формулой: 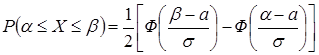 .
.
Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину 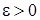 (по абсолютной величине), равна:
(по абсолютной величине), равна: 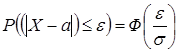 .
.
«Правило трех сигм»: если случайная величина Х имеет нормальный закон распределенияс параметрами а и 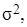 т.е.
т.е. 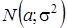 , то практически достоверно, что ее значения заключены в интервале
, то практически достоверно, что ее значения заключены в интервале 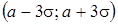 :
: 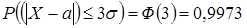 .
.
 2020-05-11
2020-05-11 95
95








