Простейшее логарифмическое уравнение 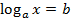 .
.
Логарифмическая функция возрастает (или убывает) на промежутке (0; 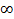 ) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любогоbданное уравнение имеет, и причем только одно, решение. Из определения логарифма числа сразу следует, что
) и принимает на этом промежутке все действительные значения. По теореме о корне отсюда следует, что для любогоbданное уравнение имеет, и причем только одно, решение. Из определения логарифма числа сразу следует, что 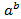 является таким решением.
является таким решением.
Пример: Решить уравнение 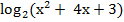 = 3.
= 3.
По определению логарифма 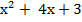 = 23
= 23
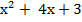 = 8
= 8
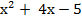 = 0
= 0
Решаем квадратное уравнение: D= 42 – 4· 1 · (–5) =36
х1 = 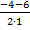 =
= 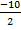 = – 5 и х2 =
= – 5 и х2 = 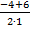 =
=  = 1.
= 1.
Следовательно, числа 1 и –5 являются решениями данного уравнения.
Ответ: –5; 1.
Пример: Решить уравнение 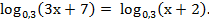
Это уравнение определено для тех значений х, при которых выполнены неравенства (выражение, стоящее под знаком логарифма должно быть больше 0):
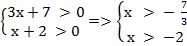 => ОДЗ: х ꞓ (−2; +∞)
=> ОДЗ: х ꞓ (−2; +∞)
Для этих х данное уравнение равносильно уравнению 3х + 7 = х + 2
3х – х = 2 – 7
2х = –5
х = –2,5.
Число х = –2,5 не входит в ОДЗ. Следовательно, данное уравнение не имеет корней.
Ответ: ø
Пример: Решить уравнение 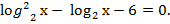
Сделаем замену переменной у = 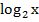 . Поэтому данное уравнение принимает вид
. Поэтому данное уравнение принимает вид
у2 – у – 6 = 0.
Решаем квадратное уравнение: D= (-1)2 – 4· 1 · (–6) =25
у1 = 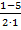 =
= 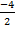 = – 2 и у2 =
= – 2 и у2 =  =
= 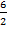 = 3.
= 3.
Получаем уравнения 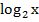 = –2
= –2 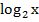 = 3
= 3
х = 2-2 х = 23
х = 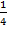 х = 8.
х = 8.
Ответ: 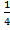 ; 8.
; 8.
2. Выполнить задания
Решите уравнения
1. 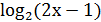 = 3
= 3
2. 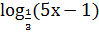 = −4
= −4
3. 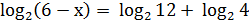
4. 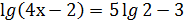
5. 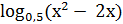 = −3
= −3
6. 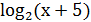 +
+ 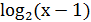 = 4
= 4
Срок сдачи задания 11.04 включительно (до 15-30).
 2020-05-11
2020-05-11 85
85







