ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4
АННОТАЦИЯ ДИСЦИПЛИНЫ МАТЕМАТИКА.. 5
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.. 7
1. Неопределенный интеграл. 8
1.1 Первообразная и неопределенный интеграл. 8
1.2 Основные свойства неопределенного интеграла. 9
1.3 Таблица интегралов. 10
1.4 Методы непосредственного интегрирования. 10
1.5 Интегрирование по частям.. 17
1.6 Интегрирование рациональных дробей. 19
1.7 Замена переменной в неопределенном интеграле. 22
1.8 Контрольные вопросы по разделу «Неопределенный интеграл». 26
1.9 Задачи для проведения промежуточного контроля усвоения материала раздела «Неопределенный интеграл». 26
2. Определенный интеграл. 27
2.1 Интегральная сумма и ее предел. Определенный интеграл. 27
2.2. Основные свойства определенного интеграла. 28
23.3 Правила вычисления определенных интегралов. 29
2.4 Интегрирование по частям.. 30
2.5 Замена переменной в определенном интеграле. 30
2.6 Приложения определенного интеграла. 31
2.7 Контрольные вопросы по разделу «Определенный интеграл». 40
2.8 Задачи для проведения промежуточного контроля усвоения материала раздела «Определенный интеграл». 40
3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ... 41
3.1 Интегралы с бесконечными пределами интегрирования. 42
3.2 Интегралы от неограниченных функций. 42
3.3 Контрольные вопросы по разделу Несобственные интегралы.. 45
3.4 Задачи для проведения промежуточного контроля усвоения материала раздела «Несобственные интегралы». 45
4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.. 45
4.1 Прямая на плоскости. 45
4.2 Кривые 2-го порядка. 48
4.3 Прямая в пространстве. Плоскости. 50
4.4 Контрольные вопросы по разделу «Аналитическая геометрия». 54
4.5 Задачи для проведения промежуточного контроля усвоения материала раздела «Аналитическая геометрия». 54
5. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 53
5.1 Дифференциальное исчисление функций двух переменных. 53
5.2 Экстремум функции 2-х переменных. 56
5.3 Наибольшее и наименьшее значения функции. 57
5.4 Градиент и производная по направлению.. 61
5.5 Контрольные вопросы по разделу «Функции нескольких переменных». 62
5.6 Задачи для проведения промежуточного контроля усвоения материала раздела «Функции нескольких переменных». 62
6. ЗАКЛЮЧЕНИЕ.. 64
7. БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 69
ВВЕДЕНИЕ
Электронное учебное пособие по дисциплине «Математика» направлено на формирование общепрофессиональных компетенций в соответствии с федеральным государственным образовательным стандартом по уровню специалитета:
- ОПК-3 Способен использовать основные законы естественнонаучных дисциплин в профессиональной деятельности;
Электронное учебное пособие предназначено для обучающихся по направлению подготовки специалитета 26.05.06 – Эксплуатация судовых энергетических установок может быть использовано при изучении других дисциплин, направленных на формирование универсальных, общепрофессиональных и профессиональных компетенций.
В электронном учебном пособии содержится материал для самостоятельной работы обучающихся по разделам и темам 2 семестра 1 курса. В эл. пособие включены следующие разделы:
1. Неопределенные интегралы,
2. Определенные интегралы,
3. Несобственные интегралы.
4. Аналитическая геометрия,
5. Функции нескольких переменных
Цель электронного учебного пособия – обеспечить возможность самостоятельной работы обучающихся во 2-ом семестре 1 курса при осуществлении перехода на дистанционные методы обучения.
Содержание данного электронного учебного пособия соответствует рабочей программе дисциплины и основано на материалах отечественных и зарубежных исследований, включая современные публикации.
Каждый раздел электронного учебного пособия включает контрольные вопросы и задания для проверки усвоения материала.
АННОТАЦИЯ ДИСЦИПЛИНЫ
МАТЕМАТИКА
Место дисциплины в структуре образовательной программы
Дисциплина относится к обязательной части блока 1. «Дисциплины (модули)» ФГОС ВО по направлению подготовки специалистов по специальности 26.05.06 «Эксплуатация судовых энергетических установок».
Дисциплина изучается по очной форме в первом, втором, третьем и четвертом семестрах.
Для освоения дисциплины необходимо знать арифметику, элементарную алгебру и геометрию в объеме среднего (полного) общего образования.
Дисциплина непосредственно предшествует дисциплинам «Физика», «Механика», «Техническая термодинамика», «Общая электротехника и электроника», «Теоретические основы электротехники», «Теория и устройство судна» и другим техническим дисциплинам профессионального цикла., для освоения других дисциплин, предусмотренных учебным планом, и решения профессиональных задач,
- применять методы, способы и средства получения, хранения, переработки математической информации,
- пользоваться при необходимости математической литературой.
Владеть:
- способностью выбирать инструментальные средства, принятые в линейной алгебре, аналитической геометрии, дифференциальном и интегральном исчислении функции одной переменной, в теории функции нескольких переменных, теории дифференциальных уравнений, в теории вероятностей и математической статистике для обработки данных в соответствии с поставленной задачей,
- основными методами решения задач линейной алгебры, аналитической геометрии, дифференциального и интегрального исчисления, функции одной переменной, функции нескольких переменных, дифференциальных уравнений, теории вероятностей и математической статистики, соответствующим математическим аппаратом,
- методами, способами и средствами получения, хранения, переработки математической информации.
Объем дисциплины по видам учебных занятий
Объем дисциплины составляет 14 зачетных единиц; всего 504 часа, из которых по очной форме 298 часа составляет контактная работа обучающегося с преподавателем
(149 часов – занятия лекционного типа, 149 часов – практические занятия).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Геометрический смысл определенного интеграла 43
Градиент................................................... 15
Длина астроиды....................................... 48
Длина дуги плоской кривой.................. 47
Длина окружности.................................. 47
достаточное условие существования неопределенного интеграла 19
Достаточное условие экстремума.......... 11
Интегральная сумма............................... 39
Каноническое уравнение гиперболы.... 60
Каноническое уравнение окружности.. 59
Каноническое уравнение параболы...... 60
Косинус угла между плоскостями......... 62
Метод неопределенных коэффициентов 31
Наименьшее и наибольшее значения функции 12
Направляющий вектор прямой.............. 61
Необходимое условие экстремума........ 11
Неопределенный интеграл..................... 19
Несобственный интеграл от неограниченной функции 54
Несобственный интеграл с бесконечными пределами 53
Общее уравнением прямой.................... 56
Объем тела вращения.............................. 49
Определенный интеграл........................ 39
Первообразная......................................... 18
Площадь плоской фигуры...................... 43
Полный дифференциал............................ 8
Правильная рациональная дробь........... 30
Производная по направлению............... 15
Расстояние от точки до прямой............. 58
Таблица интегралов................................ 21
Точка максимума.................................... 10
Точки экстремума.................................... 10
Точкой максимума.................................. 10
Угол между прямыми............................. 58
Уравнение плоскости, проходящей через прямую и точку 61
Уравнение прямой, проходящей через точку 57
Условие параллельности прямых.......... 57
Условие перпендикулярности прямых. 57
Условие существования определенного интеграла 39
Формула Ньютона-Лейбница................ 40
Функция двух переменных...................... 8
Частные производные............................... 9
Частные производные второго порядка 10
1. Неопределенный интеграл
Цель раздела: изучить теоретический материал раздела «Неопределенный интеграл» и получить практические навыки вычисления неопределенных интегралов методами непосредственного интегрирования, по частям, замены переменных и некоторыми специфическими методами, применимыми к интегралам, содержащими выражения определенного вида.
1.1 Первообразная и неопределенный интеграл
Определение 1. Функция 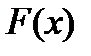 называется первообразной функции
называется первообразной функции  на промежутке
на промежутке  , если она дифференцируема во всех точках этого промежутка и выполняется равенство:
, если она дифференцируема во всех точках этого промежутка и выполняется равенство:
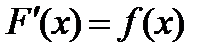 .
. 
Таким образом, первообразная  это функция, производная которой равна данной функции
это функция, производная которой равна данной функции 
Всякая непрерывная функция  имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
Теорема 1 (об общем виде первообразных).
Пусть  является первообразной для функции
является первообразной для функции  .
.
Для того чтобы другая функция 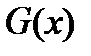 также была первообразной для
также была первообразной для  , необходимо и достаточно, чтобы она имела вид:
, необходимо и достаточно, чтобы она имела вид:  где
где  некоторое число («произвольная постоянная»).
некоторое число («произвольная постоянная»).
Проверим, что  есть также первообразная от
есть также первообразная от  ,
, 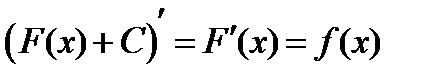 , где
, где  — произвольная постоянная.
— произвольная постоянная.
Определение 2. Пусть функция 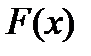 является первообразной для функции
является первообразной для функции  . Тогда выражение
. Тогда выражение  , задающее общий вид всех первообразных, называется неопределенным интегралом от функции
, задающее общий вид всех первообразных, называется неопределенным интегралом от функции 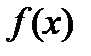 .
.
Термин «неопределенный» связан с тем, что постоянная  может принимать любое значение.
может принимать любое значение.
Неопределенный интеграл функции от  , обозначается как
, обозначается как 
Таким образом, по определению
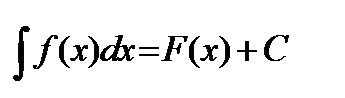 ,
, 
где  произвольная постоянная.
произвольная постоянная.
Обозначения:
· 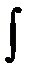 — знак неопределенного интеграла;
— знак неопределенного интеграла;
·  — подынтегральная функция;
— подынтегральная функция;
·  — переменная интегрирования;
— переменная интегрирования;
· 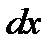 — дифференциал;
— дифференциал;
· 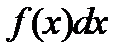 — подынтегральное выражение.
— подынтегральное выражение.
Нахождение первообразной для данной функции  называется интегрированием функции
называется интегрированием функции 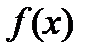 .
.
Интегрирование есть действие, обратное дифференцированию.
Интегрирование производится с помощью основных свойств неопределенного интеграла и таблицы интегралов, приведенных далее.
Таблица интегралов вытекает непосредственно из определения неопределенного интеграла и таблицы производных.
Теорема 2. ( достаточное условие существования неопределенного интеграла)
Если функция  непрерывна на некотором промежутке, то на этом промежутке для нее существует первообразная функция, а значит, и неопределенный интеграл
непрерывна на некотором промежутке, то на этом промежутке для нее существует первообразная функция, а значит, и неопределенный интеграл 
Теорема 3. (равенство неопределенных интегралов).
Два неопределенных интеграла  и
и  равны, если они задают общий вид первообразных одной и той же функции, то есть если
равны, если они задают общий вид первообразных одной и той же функции, то есть если 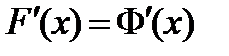 .
.
Ø Обратите внимание!
Правильность интегрирования всегдаможнопроверить, выполнив обратное действие, т.е. найдя производную функции, получившейся в результате интегрирования.
Производная должна быть равна подынтегральной функции.
| 1.2 Основные свойства неопределенного интеграла | ||||||||||||||||||||||||||||||||||
I. 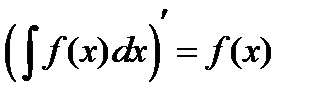 . .
| ||||||||||||||||||||||||||||||||||
II. 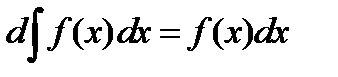 . .
| ||||||||||||||||||||||||||||||||||
III. 
| ||||||||||||||||||||||||||||||||||
IV. 
| ||||||||||||||||||||||||||||||||||
| V. VI. | ||||||||||||||||||||||||||||||||||
| 1.3 Таблица интегралов
| ||||||||||||||||||||||||||||||||||
Замечание:Свойства неопределенного интеграла и таблицу интегралов необходимо выучить наизусть.
1.4 Методы непосредственного интегрирования
Прежде чем рассматривать методы интегрирования, научимся применять табличные интегралы. Рассмотрим несколько примеров отыскания интегралов с помощью таблицы и свойств неопределенных интегралов.
Пример 1. Найти интегралы:
а) 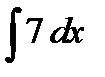 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 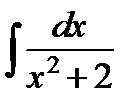 ; е)
; е) 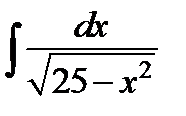 ;
;
Решение:
а) Воспользуемся табличным интегралом (2) и (V) свойством неопределенных интегралов:
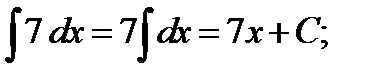
б) Воспользуемся табличным интегралом (1) и (V) свойством неопределенных интегралов:

 ;
;
в) 
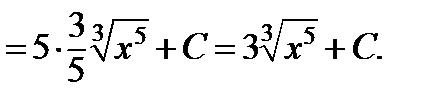
г) Представим  как
как  и воспользуемся табличным интегралом (12), где
и воспользуемся табличным интегралом (12), где  .
.
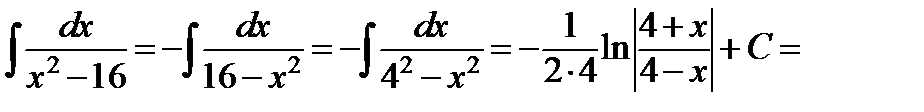

д) Преобразуем выражение в знаменателе и применим формулу (11)
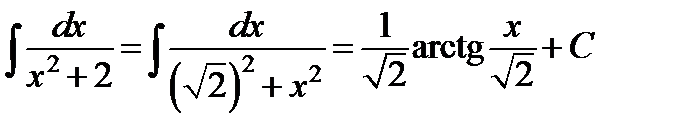 .
.
е) Преобразуем подынтегральную функцию и воспользуемся табличным интегралом
 .
.
Теперь перейдем к методам интегрирования.
Метод разложения
Этот метод применяется для интегрирования функций, представляющих собой алгебраическую сумму нескольких функций, первообразные которых заранее известны или могут быть легко получены.
Рассмотрим примеры.
Пример 2. Найти интегралы:
а)  ; б)
; б) 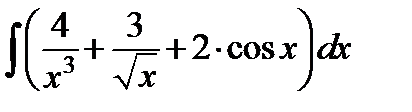 ,
,
в)  ; г)
; г) 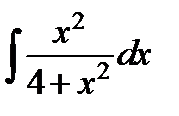 .
.
Решение:
а) 
перемножим выражения в скобках и приведем подобные члены в подынтегральном выражении, далее используем формулу (1) таблицы и свойства (IV),(V),(VI).
 =
=
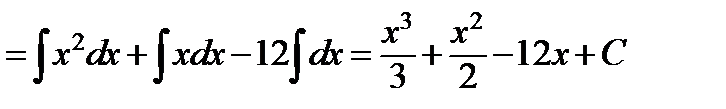 .
.
б) 
перейдем к отрицательным степеням и снова представим интеграл как сумму интегралов


в) Разделим почленно числитель на знаменатель, проведем сокращения и применим табличные интегралы



г) Прибавляя и вычитая в числителе 4, получаем
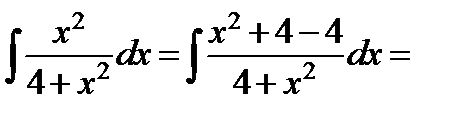
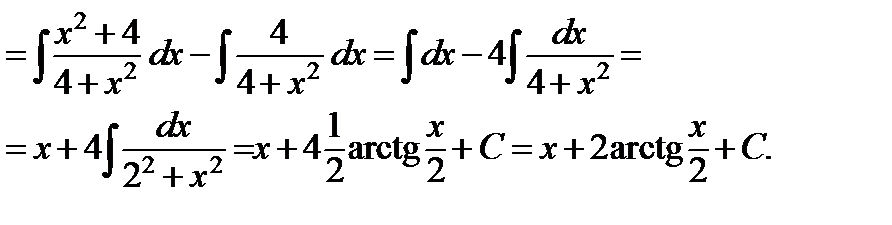
Мы разделили числитель на знаменатель таким образом, чтобы получились табличные интегралы, а потом применили таблицу интегралов.
 2020-05-21
2020-05-21 104
104
 .
. .
.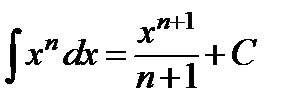 ,
,  .
.





 .
.
 .
.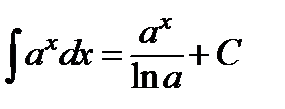 ,
, 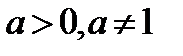
 .
. .
.
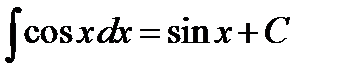 .
. .
.
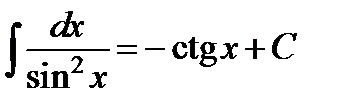 .
.
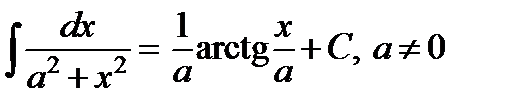 .
.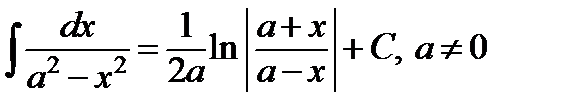 .
. .
.






