2020-05-21
159
· Если кривая 
на отрезке 
– гладкая (т.е. производная 
непрерывна), то длина дуги этой кривой, содержащейся между двумя точками 
и 
с абсциссами 
и 
, равна
. 
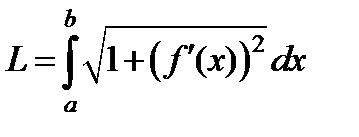· Если кривая задана уравнениями в параметрической форме 
и 
, где 
и 
непрерывно дифференцируемые функции, то длина дуги кривой равна
,
где 
и 
– значения параметра, соответствующие концам дуги.
· Если гладкая кривая задана в полярных координатах уравнением 
, 
, то длина дуги равна
Пример 11. Определить длину окружности
Решение:
Уравнение 
определяет окружность радиуса 
с центром в начале координат (рис. 9).
Рис. 9
Вычислим сначала длину четверти окружности, лежащей в первом квадранте – это дуга 
. Тогда уравнение дуги 
будет: 
. Дифференцируя это уравнение, найдем:
|
|
|
.
Тогда по формуле
= 
= 
.
Длина всей окружности равна 
.
Пример 12. Вычислить длину астроиды 
, 
( рис. 10).
Рис. 10
Решение:
Так как кривая симметрична относительно обеих координатных осей, то вычислим сначала длину ее четвертой части 
, расположенной в первом квадранте.
Дифференцируя уравнения 
и 
по переменной 
, находим:
, 
.
Для дуги 
параметр 
будет изменяться от 
до 
, следовательно,
=
Окончательно, 
.
