Аналогично определяются несобственный интеграл с бесконечным нижним пределом интегрирования

и несобственный интеграл с двумя бесконечными пределами интегрирования

где – произвольное действительное число.

Данные интегралы называют также интегралами первого рода.

С геометрической точки зрения для неотрицательной при функции несобственный интеграл представляет собой площадь фигуры, ограниченной сверху графиком функции слева отрезком прямой снизу осью

3.2 Интегралы от неограниченных функций.

Пусть функция непрерывна для всех значений , кроме точки в которой имеет бесконечный разрыв.

Определение 1. Н есобственный интеграл от неограниченной функции (или несобственный интеграл второго рода) определяется так:

где произвольная бесконечно малая величина.

Определение 2. Если оба предела в правой части этого равенства существуют, то несобственный интеграл называется сходящимся. В противном случае (т.е. если не существует хотя бы один из указанных пределов) – расходящимся.

При и несобственные интегралы равны

Пример 4. Вычислить несобственный интеграл или доказать его расходимость: .

Решение:

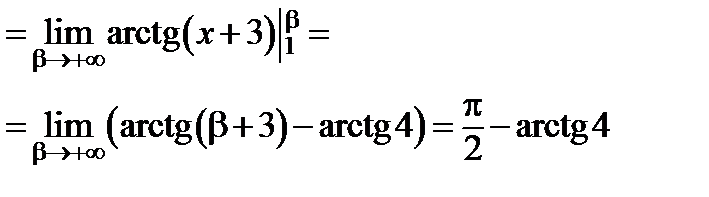
Таким образом, несобственный интеграл сходится, и его значение равно .

При нахождении последнего предела мы воспользовались тем, что .

Пример 5. Вычислить несобственный интеграл или доказать его расходимость:

Решение:

Учитывая, что , так что , имеем:

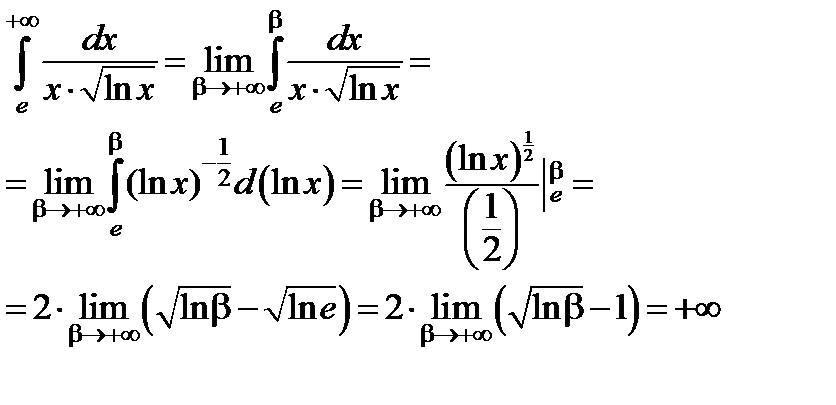
поскольку ; (см. рис.13, 14).

Рис. 13 Рис. 14

Конечного предела не существует, поэтому несобственный интеграл расходится.

Пример 6. Вычислить несобственный интеграл или доказать его расходимость: .

Решение:

Поскольку в точке принадлежащей промежутку интегрирования, функция терпит бесконечный разрыв, то интеграл относится к несобственным интегралам второго рода и вычисляется по формуле

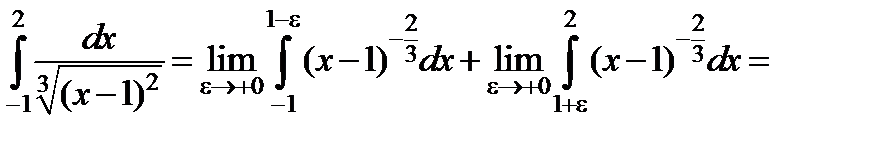
Следовательно, данный интеграл сходится и его значение равно

3.3 Контрольные вопросы по разделу Несобственные интегралы

1. Несобственные интегралы с бесконечными пределами.

2. Несобственные интегралы по конечному промежутку.

3.4 Задачи для проведения промежуточного контроля усвоения материала раздела «Несобственные интегралы»

Задание 22. Вычислить несобственный интеграл.

1. .	2. .
3. .	4. .
5. .	6. .
7. .	8. .
9. .	10. .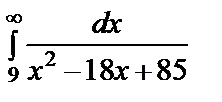

Задание 23. Вычислитьнесобственный интеграл или доказать его расходимость .

№ варианта	1	2	3	4	5	6	7	8	9	10
a	1	2	3	4	5	6	7	8	9	10
b	10	9	8	7	6	5	4	3	2	1

4 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

4.1 Прямая на плоскости

Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 — прямая проходит через начало координат;

• А = 0, В ≠0, С ≠0 { By + C = 0} — прямая параллельна оси Ох;

• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} — прямая параллельна оси Оу;

• В = С = 0, А ≠0 — прямая совпадает с осью Оу;

• А = С = 0, В ≠0 — прямая совпадает с осью Ох.

Уравнение прямой может быть представлено в различном виде в зависимости от каких-либо заданных начальных условий.

Задача 1

Составить уравнение прямой, проходящей через точку

а) параллельно прямой ;

б) перпендикулярно прямой .

Решение

Прямая задана своим общим уравнением. Представим уравнение прямой в задании в виде уравнения прямой с угловым коэффициентом, т. е. в виде . Для этого выразим из заданного уравнения. Решаем:

Получили — угловой коэффициент прямой.

Теперь продолжим решение задачи отдельно для каждого случая.

1. Воспользуемся условием параллельности прямых: если две прямые и параллельны, то их угловые коэффициенты равны, т. е.

Из этого следует, что прямая, проходящая через точку параллельно прямой , имеет угловой коэффициент, равный , т. е. Запишем , т. е. мы получили семейство прямых, параллельных заданной прямой. Нам необходимо выбрать только одну. Для этого в условии даны координаты точки Подставим эти координаты в уравнение прямой и найдем :

Исходя из этого, можно записать уравнение параллельной прямой . Обе прямые изображены на рисунке:

2. Воспользуемся условием перпендикулярности прямых: если две прямые 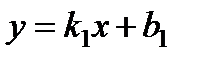и перпендикулярны, то их угловые коэффициенты связаны следующим образом:

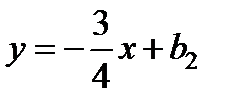Из этого следует, что прямая, проходящая через точку перпендикулярно прямой , имеет угловой коэффициент (). Запишем , т. е. мы получили семейство прямых, перпендикулярных заданной прямой. Нам необходимо выбрать только одну. Для этого в условии даны координаты точки . Подставим эти координаты в уравнение прямой и найдем :

Исходя из этого можем записать уравнение прямой, перпендикулярной данной:

Обе прямые изображены на рисунке:

Задача 2

Для прямых:

найти их взаимное расположение. В случае их пересечения найти угол между ними, в случае их параллельности — расстояние.

Если две прямые заданы общими уравнениями и , то могут представиться три случая:

а) 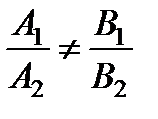— прямые имеют одну общую точку (пересекаются);

б) — прямые параллельны (условие параллельности прямых);

в) — прямые сливаются, т. е. оба уравнения определяют одну и ту же прямую.

Также имеет место условие ортогональности (перпендикулярности) прямых

Расстояние от точки до прямой находим по формуле

Угол между прямыми и находим по формуле

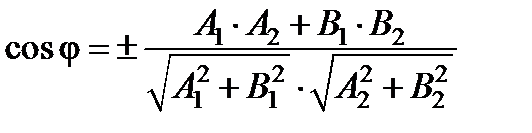Решение

Исследуем прямые из пункта 1):

Для данных прямых имеем:

Следовательно,

; ; ,

значит, прямые имеют одну общую точку (пересекаются). Найдем угол между этими прямыми:

Исследуем прямые из 2):

Для данных прямых имеем

Получаем:

; ; .

Следовательно,

и данные прямые параллельны.

Искомое расстояние найдем как расстояние от произвольной точки первой прямой до второй прямой. Возьмем на первой прямой произвольную точку, например, точку с абсциссой . Ее ордината будет Итак, на первой прямой выбрана точка .