В основе следующих способов интегрирования лежит свойство инвариантности формул интегрирования, которое заключается в следующем:
если 
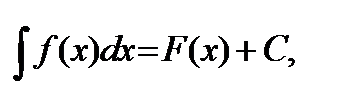 то
то
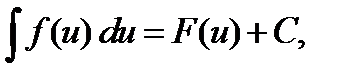
где 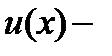 произвольная дифференцируемая функция от
произвольная дифференцируемая функция от 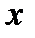 .
.
Внесение постоянного множителя под знак дифференциала.
Согласно определению дифференциала, если 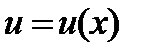
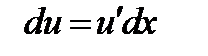 ,
, 
тогда 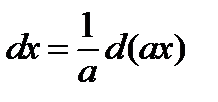 ,
,
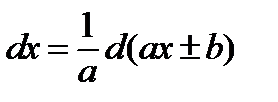
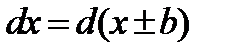 ;
;
Ø Обратите внимание! Интегралы рассмотренные далее однотипны: каждый из них может быть найден путем применения формулы к табличным интегралам.
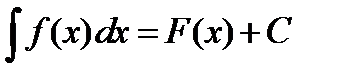
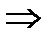
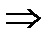
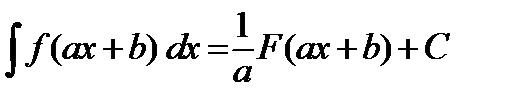
Пример 3. Найти интегралы:
а) 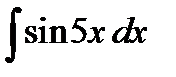 ; б)
; б) 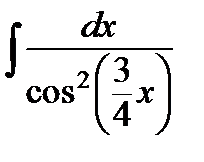 ; в)
; в) 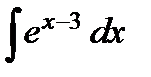 ;
;
г) 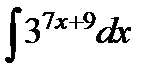 ; д)
; д) 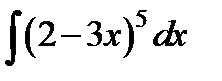 ; е)
; е) 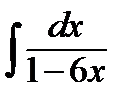 ;
;
ж) 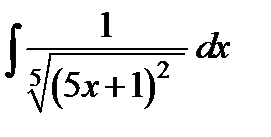 ; з)
; з) 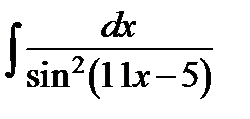 ;
;
и) 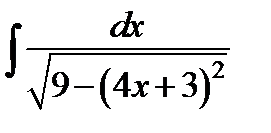 ; к)
; к) 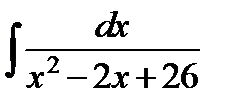 .
.
Решение:
а) 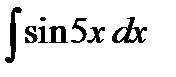 ;
;
Данный интеграл окажется табличным, если под знаком дифференциала
будет находиться аргумент 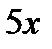 подынтегральной функции
подынтегральной функции 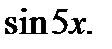
Так как 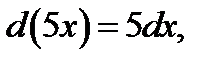 то
то
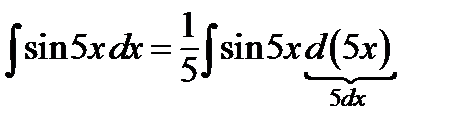 .
.
Следовательно, подстановка 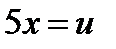 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
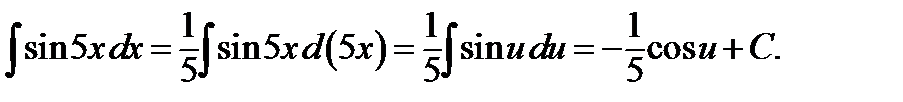
Возвращаясь к старой переменной, окончательно получим
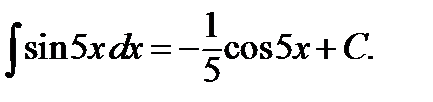
б) 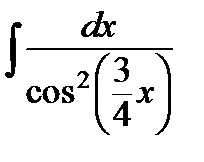 ;
;
Проведем преобразования, аналогичные преобразованиям в предыдущем интеграле. Отличие состоит лишь в том, что под дифференциал вносится дробное число.
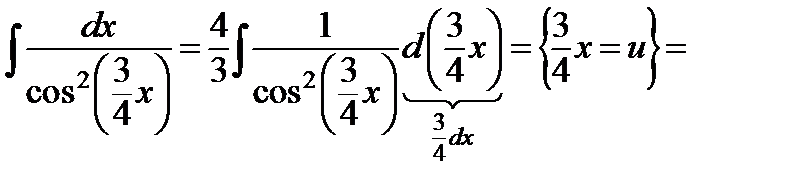
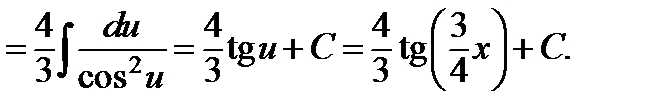
в) 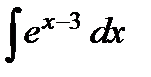 ;
;
Для того чтобы данный интеграл стал табличным необходимо под знаком дифференциала получить выражение 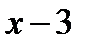 , которое является аргументом подынтегральной функции
, которое является аргументом подынтегральной функции 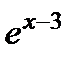 .
.
Для этого используем формулу
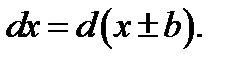
Следовательно, 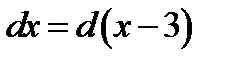 и искомый интеграл имеет вид
и искомый интеграл имеет вид
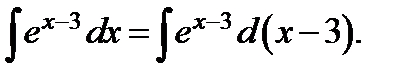
Подстановка 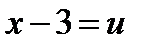 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
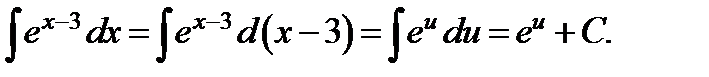
Или, возвращаясь к старой переменной,
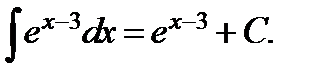
г) 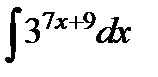 ;
;
В данном примере для преобразования под знаком дифференциалаприменим формулу
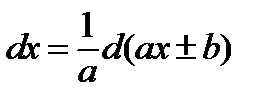 .
.
Так как 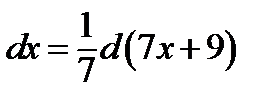 , то
, то
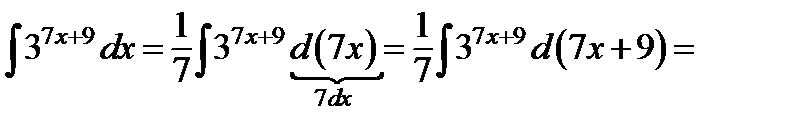
Следовательно, подстановка 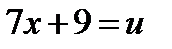 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
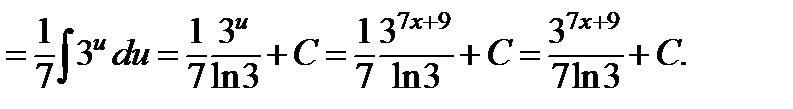
д) 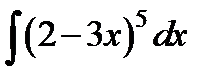 ;
;
Проведем преобразования дифференциала:
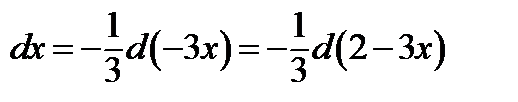
Тогда интеграл приобретает вид:
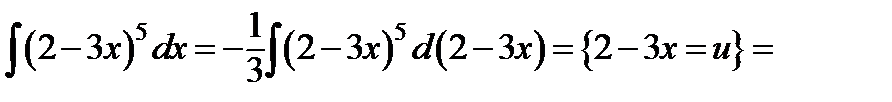
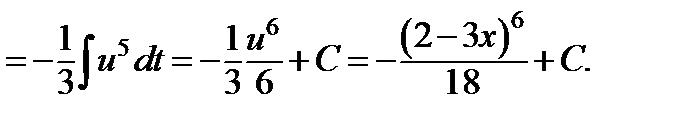
е) 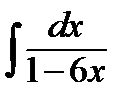 ;
;
В данном случае преобразования дифференциала имеют вид:
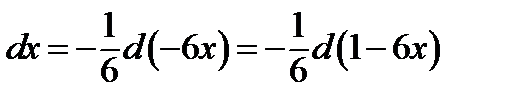
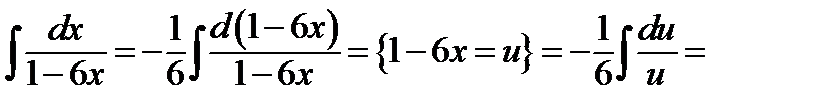


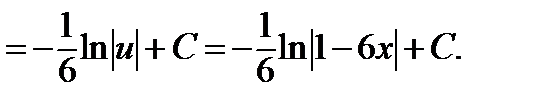
ж) 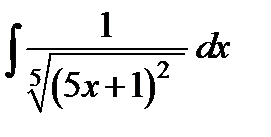 ;
;
Имеем 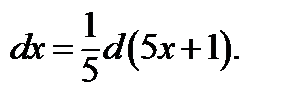 Следовательно,
Следовательно,
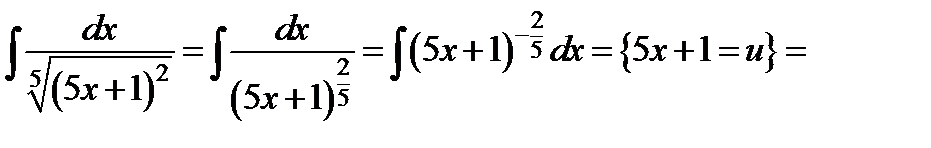
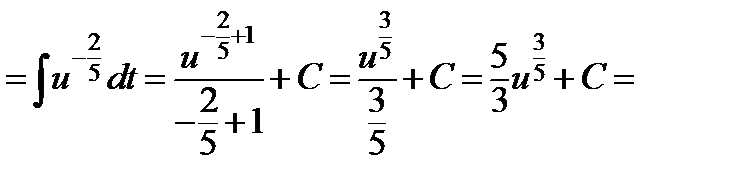
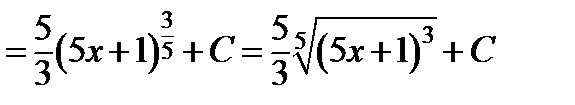 .
.
и) 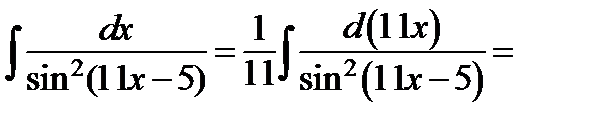
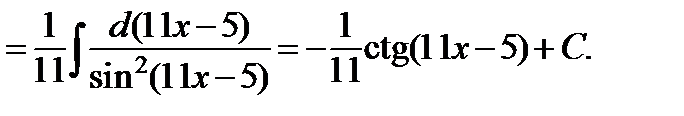
и) 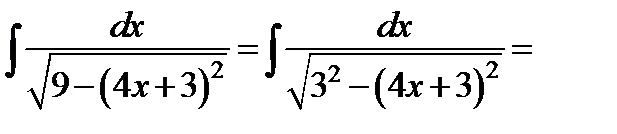
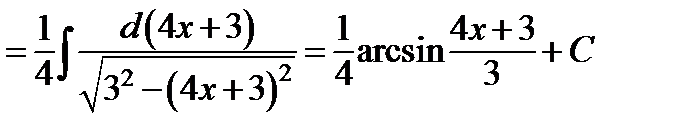
к) 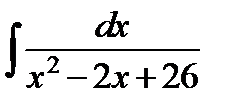 ;
;
Выделим полный квадрат в знаменателе подынтегральной дроби
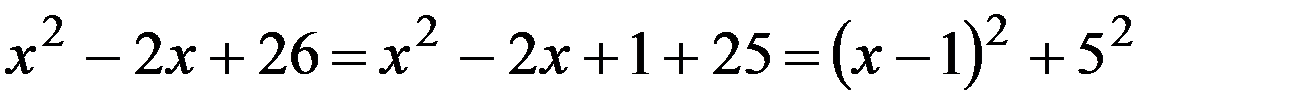 ,
,
Тогда,
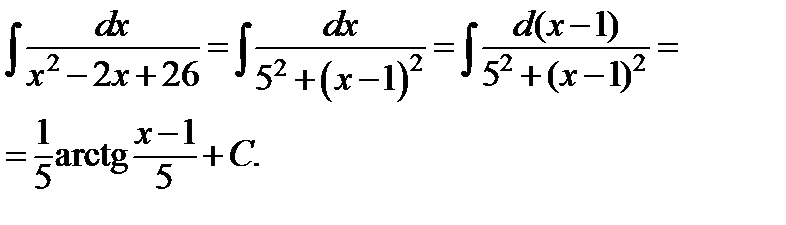 .
.
 2020-05-21
2020-05-21 149
149








