2020-05-21
143
Множество значений дискретной случайной величины представляет собой конечную или бесконечную числовую последовательность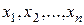 
. При этом, вероятность того что случайная величина примет какое-либо конкретное значение 
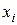обозначается символом: 
.
Определение. Функцией распределения случайной величины 
называется функция 
, которая, для каждого значения 
выражает вероятность того, что случайная величина 
примет значение меньшее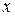 
., т.е. 
.
Пример 31. Анализируется прибыль 
(%) предприятий отрасли. Результаты обследования 
предприятий занесены в следующий вариационный ряд:
| 5 | 10 | 15 | 20 | 25 |
| 5 | 20 | 40 | 25 | 10 |
| 0,05 | 0,2 | 0,4 | 0,25 | 0,1 |
Необходимо определить функцию распределения и построить ее график.
Решение:
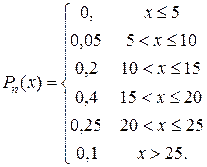
Замечание. Стрелки могут быть слева от граничных линий в зависимости от условий задачи.
Согласно данному примеру, можно утверждать, что функция распределения любой дискретной случайной величины представляет собой разрывную ступенчатую функцию, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции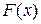 
равна единице.
|
|
|
Приведем некоторые свойства функции распределения.
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: 
;
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси: 
; 
;
3. Вероятность попадания случайной величины в интервал 
(включая 
) равна приращению ее функции распределения на этом интервале:
Замечание: Свойства функции распределения для дискретных и непрерывных случайных величин одинаковы.
