Определение. Непрерывной называется такая случайная величина  , для которой функция распределения непрерывна.
, для которой функция распределения непрерывна.
В данном случае, производную от функции распределения случайной величины называют плотностью распределения вероятности.

В отличии от функции распределения, понятие плотность вероятности существует только для непрерывных случайных величин. Плотность вероятности непрерывной случайной величины обладает следующими свойствами.
1. Плотность вероятности – неотрицательная функция, т.е.  ;
;
2. Вероятность попадания непрерывной случайной величины в интервал  равна определенному интегралу от ее плотности вероятности в пределах от
равна определенному интегралу от ее плотности вероятности в пределах от  до
до 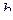 , т.е.
, т.е.  .
.
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по следующей формуле:
 .
.
4. Интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице.  .
.
Приведем основные числовые характеристики непрерывных случайных величин.
Математическим ожиданием непрерывной случайной величины  с плотностью вероятности
с плотностью вероятности  называется следующий определенный интеграл
называется следующий определенный интеграл 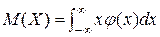 .
.
–Дисперсия:
Дисперсией непрерывной случайной величины  называется математическое ожидание квадрата ее отклонения от среднего значения.
называется математическое ожидание квадрата ее отклонения от среднего значения.
 ,
,
однако, оказывается удобнее вычислять по формуле
 .
.
–Среднее квадратическое отклонение:
Средним квадратическим отклонением непрерывной случайной величины принято называть корень квадратный из дисперсии

Если  представляет собой функцию случайного аргумента
представляет собой функцию случайного аргумента  , который имеет плотность вероятности
, который имеет плотность вероятности  , то математическое ожидание и дисперсия случайной величины
, то математическое ожидание и дисперсия случайной величины  находятся по следующим формулам:
находятся по следующим формулам:


Пример 32. Случайная величина  задана плотностью вероятности
задана плотностью вероятности  в интервале
в интервале  , вне этого интервала
, вне этого интервала  . Требуется определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины
. Требуется определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины  .
.
Решение: Математическое ожидание:
 ;
;
Дисперсия:  ;
;
Среднее квадратическое отклонение:
 .
.
Пример 33. Дана плотность вероятности непрерывной случайной величины  :
:

Найти интегральную функцию  , предварительно вычислив значение параметра
, предварительно вычислив значение параметра  .
.
Решение: Поскольку все значения случайной величины  принадлежат интервалу
принадлежат интервалу  . то
. то  .
.
Интегральная функция определяется следующим образом:
При 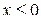 ,
, 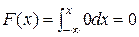 ;
;
При 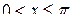 ,
,  ;
;
При  ,
, 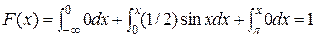 .
.
Следовательно:

Пример 34. Случайная величина  задана плотностью вероятности
задана плотностью вероятности 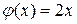 в интервале
в интервале  , вне этого интервала
, вне этого интервала  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.
Решение: Искомые величины определяются по представленным выше формулам:
 ;
; 
3.6 Задачи для самостоятельного решения
121. [2] Дана интегральная функция распределения случайной величины  :
:

Найти плотность вероятности  .
.
Ответ:

122. [2] Дана плотность вероятности случайной величины  :
:

Найти параметр  . (Ответ:.
. (Ответ:.  ).
).
123. [2] Случайная величина  , принимающая положительные значения, имеет плотность вероятности
, принимающая положительные значения, имеет плотность вероятности  . Найти границы значений случайной величины
. Найти границы значений случайной величины  , параметр
, параметр  и математическое ожидание случайной величины
и математическое ожидание случайной величины  . (Ответ.
. (Ответ.  ;
;  ;
; 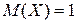 ).
).
124. [2] Случайная величина  имеет равномерное распределение вероятностей на интервале ]4;10[. Найти ее математическое ожидание, дисперсию и среднее квадратическое отклонение. (Ответ:
имеет равномерное распределение вероятностей на интервале ]4;10[. Найти ее математическое ожидание, дисперсию и среднее квадратическое отклонение. (Ответ:  ;
;  ;
;  ).
).
125. [2] Случайная величина  имеет равномерное распределение вероятностей. Найти плотность вероятности, если математическое ожидание случайной величины
имеет равномерное распределение вероятностей. Найти плотность вероятности, если математическое ожидание случайной величины  равно 8, а дисперсия равна (1/3). Ответ:
равно 8, а дисперсия равна (1/3). Ответ:

126. [2] Два действительных числа  и
и  выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность того, что сумма этих квадратов окажется больше 64? (Ответ:
выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность того, что сумма этих квадратов окажется больше 64? (Ответ:  ).
).
127. [2] Из фиксированной вершины квадрата со стороной  произвольным радиусом, меньшим его диагонали, проведена окружность. Какова вероятность того, что она пересечет стороны квадрата, которым принадлежит данная вершина? (Ответ:
произвольным радиусом, меньшим его диагонали, проведена окружность. Какова вероятность того, что она пересечет стороны квадрата, которым принадлежит данная вершина? (Ответ:  ).
).
128. [2] В равносторонний треугольник, сторона которого равна  , вписан круг. Внутри треугольника независимо друг от друга наудачу выбираются 5 точек. Какова вероятность того, что 3 из этих точек окажутся внутри круга? (Ответ:
, вписан круг. Внутри треугольника независимо друг от друга наудачу выбираются 5 точек. Какова вероятность того, что 3 из этих точек окажутся внутри круга? (Ответ:  ).
).
129. [2] Закон равномерного распределения вероятностей случайной величины 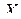 задан плотностью вероятности
задан плотностью вероятности

Найти интегральную функцию случайной величины 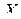 . Ответ:.
. Ответ:.
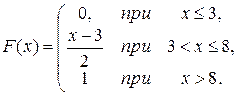
130. [1] Плотность распределения непрерывной случайной величины  в интервале ]0,
в интервале ]0,  [ равна
[ равна  ; вне этого интервала
; вне этого интервала  . Найти постоянный параметр
. Найти постоянный параметр  . (Отве:
. (Отве:  ).
).
131. [1] Непрерывная случайная величина  в интервале ]0,
в интервале ]0,  [ задана плотностью распределения
[ задана плотностью распределения 
 ; вне этого интервала
; вне этого интервала 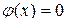 . Найти вероятность того, что
. Найти вероятность того, что  примет значение, принадлежащее интервалу ]1, 2[. (Ответ:
примет значение, принадлежащее интервалу ]1, 2[. (Ответ:  ).
).
132. [1] Задана плотность распределения непрерывной случайной величины  :
:

Найти функцию распределения  . Ответ:
. Ответ:

133. [1] Плотность распределения непрерывной случайной величины  в интервале ]
в интервале ] 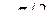 ,
,  [ равна
[ равна  ; вне этого интервала
; вне этого интервала  . Найти вероятность того, что в трех независимых испытаниях
. Найти вероятность того, что в трех независимых испытаниях  примет ровно два раза значение, заключенное в интервале
примет ровно два раза значение, заключенное в интервале
] 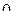 ,
,  [.
[.
(Ответ:.  ;
;  ).
).
134. [1] Случайная величина  задана плотностью распределения
задана плотностью распределения  в интервале ]
в интервале ] 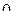 ,
,  [; вне этого интервала
[; вне этого интервала  . Найти математическое ожидание величины
. Найти математическое ожидание величины  . (Ответ:
. (Ответ:  ).
).
135. [1] Случайная величина  в интервале ]
в интервале ]  ,
,  [ задана плотностью распределения
[ задана плотностью распределения  ; вне этого интервала
; вне этого интервала  . Найти дисперсию
. Найти дисперсию  . (Ответ:
. (Ответ:  ).
).
136. [1] Авттобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин. (Ответ.  ).
).
137. [1] Найти дисперсию и среднее квадратическое отклонение случайной величины  , распределенной равномерно в интервале ]2, 8[ (Ответ:
, распределенной равномерно в интервале ]2, 8[ (Ответ:  ;
;  ).
).
138. [1] Закон равномерного распределения задан плотностью вероятности  в интервале ]
в интервале ]  ,
,  [; вне этого интервала
[; вне этого интервала  . Найти функцию распределения
. Найти функцию распределения  . Ответ:
. Ответ:

139. [1] Минутная стрелка кварцевых часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с. (Ответ:.  ).
).
140. [4] Дана функция

При каком значении параметра  эта функция является плотностью распределения некоторой некоторой непрерывной случайной величины
эта функция является плотностью распределения некоторой некоторой непрерывной случайной величины  ? Найти математическое ожидание и дисперсию случайной величины
? Найти математическое ожидание и дисперсию случайной величины  . (Ответ:
. (Ответ:  ;
; 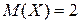 ;
;  ).
).
141. [4] Случайная величина  задана функцией распределения
задана функцией распределения

Найти: а) плотность вероятности  ; б) математическое ожидание
; б) математическое ожидание  ; в) дисперсию
; в) дисперсию 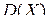 . (Ответ:.
. (Ответ:.  {0 при
{0 при  и при
и при  ;
;  при.
при.  }; б)
}; б) 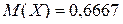 ; в)
; в)  ; г)
; г)  ;
;  ;
;  ).
).
142. [4] Случайная величина  , сосредоточенная на интервале ]
, сосредоточенная на интервале ]  ,
,  [, задана квадратичной функцией распределения
[, задана квадратичной функцией распределения  , имеющей максимум при
, имеющей максимум при  . Найти параметры
. Найти параметры 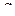 ,
,  и
и  и вычислить вероятность попадания случайной величины
и вычислить вероятность попадания случайной величины  в интервал [2;3]. (Ответ:
в интервал [2;3]. (Ответ:  ;
; 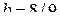 ;
;  ;
;  ).
).
143. [4] Случайная величина  , сосредоточенная на интервале [-
, сосредоточенная на интервале [-  , 3], задана функцией распределения
, 3], задана функцией распределения  . Найти вероятность попадания случайной величины
. Найти вероятность попадания случайной величины  в интервал [0;2]. Построить график функции
в интервал [0;2]. Построить график функции  . (Ответ:
. (Ответ:  ).
).
144. [4] Случайная величина  , сосредоточенная на интервале [2, 6], задана функцией распределения
, сосредоточенная на интервале [2, 6], задана функцией распределения  . Найти вероятность того, что случайная величина
. Найти вероятность того, что случайная величина  примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6. Ответ:.
примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6. Ответ:.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
145. [5] При каких значениях параметров  и
и  функция
функция

Может быть функцией распределения некоторой непрерывной случайной величины  ? Найти вероятность того, что случайная величина
? Найти вероятность того, что случайная величина 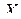 примет значение заключенное в промежутке ]-2,3, 1,5[. Построить график распределения этой случайной величины. (Ответ:
примет значение заключенное в промежутке ]-2,3, 1,5[. Построить график распределения этой случайной величины. (Ответ:  ,
,  ;
;  ).
).
146. [5] Задана функция распределения непрерывной случайной величины 

Найти: а) значения постоянных 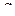 и
и  ; б) плотность распределения
; б) плотность распределения  случайной величины
случайной величины  . (Ответ: а)
. (Ответ: а)  ,.
,.  ; б)
; б)  при
при  и
и  в остальных случаях).
в остальных случаях).
147. [5] Случайная величина  задана функцией распределения
задана функцией распределения

Найти: а) плотность распределения  случайной величины
случайной величины 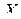 ; б) вероятность того, что случайная величина
; б) вероятность того, что случайная величина  в результате опыта примет значения в интервале ]-1,1[. Ответ:
в результате опыта примет значения в интервале ]-1,1[. Ответ:
а)  б)
б)  .
.
148. [5] Задана функция

Определить: а) при каком значении 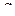 функция
функция  будет функцией распределения случайной величины
будет функцией распределения случайной величины  ; б) плотность вероятности случайной величины
; б) плотность вероятности случайной величины  . (Ответ: а).
. (Ответ: а).  ; б). 9/16 ).
; б). 9/16 ).
149. [5] Дана функция распределения непрерывной случайной величины 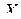

Функция  при
при  имеет максимум. Найти: а) параметры
имеет максимум. Найти: а) параметры 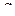 ,
,  ,
,  ; в) вероятности событий
; в) вероятности событий  ,
,  . (Ответ.:а)
. (Ответ.:а)  ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ).
).
150. [3] Случайная величина  распределена равномерно.
распределена равномерно.  ,
,  . Найти плотность величины
. Найти плотность величины  . (Ответ:
. (Ответ:  при
при  , и
, и  вне этого интервала).
вне этого интервала).
151. [3] Найти математическое ожидание и дисперсию двух независимых случайных величин  и
и  , равномерно распределенных соответственно в промежутках
, равномерно распределенных соответственно в промежутках 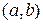 и
и  . Ответ:
. Ответ:  ;
;
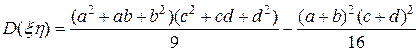 .
.
152. [3] Точка брошена наудачу внутрь круга радиуса  . Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади области. Найти функцию распределения, математическое ожидание и дисперсию расстояния точки до центра круга. Ответ:.
. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади области. Найти функцию распределения, математическое ожидание и дисперсию расстояния точки до центра круга. Ответ:.
 ,
,  ;
;  .
.
153. [3] Случайная величина  равномерно распределена на отрезке
равномерно распределена на отрезке  ;
;  ;
; 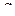 и
и  положительные постоянные. Найти математическое ожидание и дисперсию величины
положительные постоянные. Найти математическое ожидание и дисперсию величины  . Ответ:
. Ответ:
 ;
;

154. [3] Мишень состоит из трех концентрических кругов с радиусами 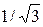 ,
,  и
и 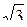 . Попадание в центральный круг стоит 4 очка, в среднее кольцо – 3 очка, в крайнее кольцо – 2 и вне круга – 0 очков. Вероятность попадания на расстоянии
. Попадание в центральный круг стоит 4 очка, в среднее кольцо – 3 очка, в крайнее кольцо – 2 и вне круга – 0 очков. Вероятность попадания на расстоянии  от центра мишени равна
от центра мишени равна  . Найти математическое ожидание числа очков, выбитых при пяти выстрелах. (Ответ:
. Найти математическое ожидание числа очков, выбитых при пяти выстрелах. (Ответ:  ).
).
155. [3] Случайная величина  имеет плотность
имеет плотность

Найти математическое ожидание и дисперсию величины  . (Ответ:
. (Ответ:  ;
;  ).
).
156. [3] Пусть  есть число появлений события
есть число появлений события  в серии
в серии  независимых испытаний, в каждом из которых
независимых испытаний, в каждом из которых  . Найти
. Найти  и
и  . (Ответ:
. (Ответ:  ;.
;.  ).
).
157. [6] Обвал одинаково возможен в любой точке на горной дороге от 30-го км до 90-го км. Вероятность того, что обвал произойдет в интервале от конца или начала дороги равен 1/5. Найти эти интервалы. (Ответ: а).(30; 36); б) (84; 90)).
158. [6] Найти параметр  распределения: а) заданного плотностью
распределения: а) заданного плотностью

б) заданного функцией распределения

(Ответ: а).  ; б)
; б)  ).
).
159. [6] Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 60 с. Найти плотность и функцию распределения этой случайной величины. Определить вероятность того, что время ожидания ответа не превысит 45 с. Ответ:.
 .
. 
 2020-05-21
2020-05-21 3583
3583
