Определение 1 Соответствие между возможными значениями 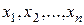 дискретной случайной величины
дискретной случайной величины 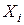 (
(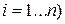 и соответствующими им вероятностями
и соответствующими им вероятностями 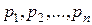 представляет собой закон распределения этой величины.
представляет собой закон распределения этой величины.
Закон распределения может быть задан в виде таблицы:
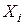
| 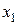
| 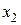
| … | 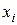
| … | 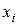
|
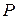
| 
| 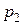
| … | 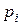
| … | 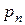
|
Поскольку события 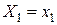 ,
, 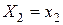 ,…
,… 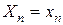 образуют полную группу, то:
образуют полную группу, то: 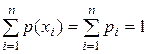 .
.
Приведем некоторые наиболее часто встречающиеся законы распределения случайных величин.
1. Равномерное распределение вероятности случайной величины 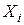 принимающей
принимающей 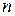
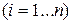 значений
значений
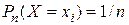
Пример 26. Составить закон распределения числа выпавших очков при одном подбрасывании игральной кости (кубика).
Решение: По условию случайная величина 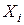
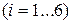 - количество выпавших очков. Следовательно,
- количество выпавших очков. Следовательно, 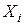 имеет 6 различных значений, поскольку на каждой грани разное число очков:
имеет 6 различных значений, поскольку на каждой грани разное число очков: 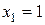 ,
, 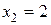 ,
, 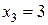 ,
, 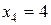 ,
, 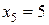 ,
, 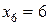 .
.
Вероятности выпадения этих случайных величин равны вероятности появления одной грани, то есть 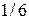 , следовательно, закон распределения имеет вид:
, следовательно, закон распределения имеет вид:
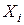
| 1 | 2 | 3 | 4 | 5 | 6 |
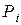
| 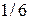
| 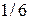
| 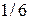
| 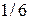
| 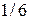
| 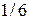
|
Очевидно, что 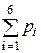 = 1.
= 1.
Пример 27. Денежная лотерея содержит 10000 билетов, причем 1 билет выигрывает 1000 руб., 10 билетов - по 100 руб., а 100 билетов - по 1 руб. Составить закон распределения величины случайного выигрыша на один лотерейный билет.
Решение: В данном случае, случайной величиной 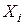
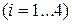 является величина выигрыша на один лотерейный билет. Она имеет следующие значения
является величина выигрыша на один лотерейный билет. Она имеет следующие значения 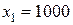 ,
, 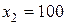 ,
, 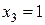 ,
, 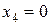 , тогда:
, тогда: 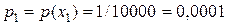 ;
; 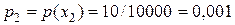 ;
; 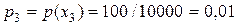 ;
; 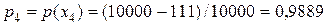
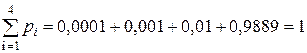
Следовательно, закон распределения величины выигрыша на 1 лотерейный билет будет иметь следующий вид:
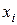
| 1000 | 100 | 1 | 0 |
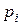
| 0,0001 | 0,001 | 0,01 | 0,9889 |
2. Биномиальное распределение вероятности случайной величины 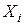 , значениями которой являются возможные значения числа
, значениями которой являются возможные значения числа 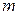 появления события
появления события 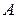 при проведении
при проведении 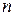 повторных независимых испытаний задается формулой Бернулли
повторных независимых испытаний задается формулой Бернулли
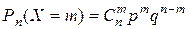 , где
, где 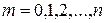 .
.
В табличной форме:
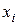
| 0 | 1 | 2 | … | 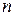
|
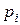
| 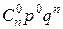
| 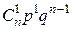
| 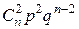
| … | 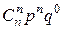
|
Такое название данный закон распределения получил в связи с тем, что вероятности 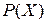 совпадают с соответствующими слагаемыми бинома Ньютона:
совпадают с соответствующими слагаемыми бинома Ньютона:
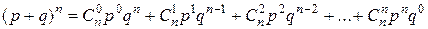 .
.
А поскольку 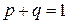 , то сумма вероятностей
, то сумма вероятностей 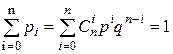 .
.
Пример 28. Монета подброшена два раза. Составить закон распределения числа появлений герба.
Решение: Случайной величиной 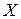 будет число появлений герба при двукратном подбрасывании монеты. Очевидно, что герб может появиться от 0 до 2 раз, то есть случайная величина
будет число появлений герба при двукратном подбрасывании монеты. Очевидно, что герб может появиться от 0 до 2 раз, то есть случайная величина 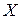 принимает значения
принимает значения  ;
; 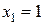 ;
; 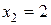 , тогда:
, тогда:
 ;
; 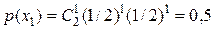 ;
;
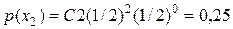 , т. к.
, т. к. 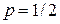 ,
, 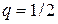
Тогда закон распределения имеет вид:
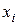
| 0 | 1 | 2 |
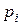
| 0,25 | 0,5 | 0,25 |
Сделаем проверку: 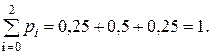 .
.
2. Распределение Пуассона
Предположим что имеется случайная величина 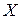 , которая представляет собой число появлений некоторого события
, которая представляет собой число появлений некоторого события 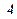 при
при 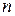 независимых испытаниях. В каждом таком испытании, вероятность появления события
независимых испытаниях. В каждом таком испытании, вероятность появления события 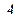 очень мала, т. е.
очень мала, т. е. 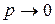 . Случайная величина
. Случайная величина 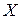 может принимать значения от 0 до
может принимать значения от 0 до 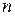 , а вероятность ее наступления определяется по следующей формуле
, а вероятность ее наступления определяется по следующей формуле
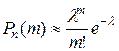 , где
, где 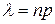
известной как формула Пуассона.
При этом, закон распределения случайной величины 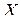 , представленный в табличной форме, имеет следующий вид:
, представленный в табличной форме, имеет следующий вид:
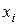
| 0 | 1 | 2 | … | n |
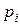
| 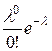
| 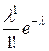
| 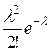
| … | 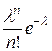
|
называется распределением Пуассона.
Пример 29. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что изделие повредится во время транспортировки, составляет 0,0002. Найти вероятность того, что на базу прибудут 3 поврежденных изделия.
Решение. По условию задачи, 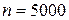 ,
, 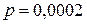 ,
, 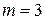 . Следовательно
. Следовательно 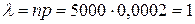 .
.
По формуле Пуассона: 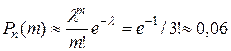 .
.
 2020-05-21
2020-05-21 200
200








