Раздел 4. Закон больших чисел

Неравенство Маркова.

    Если случайная величина принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа  верно неравенство

                       ,                                   (22)

отсюда                                                (23)

Неравенство Чебышева

Если случайная величина имеет конечную дисперсию 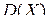 и математическое ожидание , то для любого положительного числа  справедливо следующее неравенство

                                                    (24)

т. е., вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине меньше положительного числа , не меньше чем .

Из последнего неравенства:

Теорема Чебышева.

Теорема Чебышева. Если последовательность независимых случайных величин , ,…,  с математическими ожиданиями  и дисперсиями  (, ограничены одной и той же постоянной , то для любого положительного числа  выполняется следующее равенство:

(25)

т. е., при указанных выше условиях, средняя арифметическая случайных величин , ,…,  сходится по вероятности к средней арифметической их математических ожиданий , ,…, . Принято говорит что последовательность , ,…,  подчиняется закону больших чисол.

    При доказательстве теоремы Чебышева, получается следующая оценка

    (26)

Следствие. В том случае, если в условии теоремы Чебышева случайные величины , ,…,  имеют одно и то же математическое ожидание , то формулы (25) и (26) принимают вид:

;

                                       (27)

 

Теорема Бернулли

Теорема Бернулли. В том случае, если в каждом из 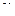 независимых испытаний вероятность  появления события  постоянна, то при для любого сколь угодно малого положительного  выполняется равенство:

где () – относительная частота появления события .

    При доказательстве теоремы Бернулли, получается следующая оценка

                                                                (28)

где ; .