Получение точечных и интервальных статистических оценок

Построение интервального статистического ряда

На первом этапе следует по заданной выборке 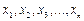  объема n построить интервальный (группированный ) статистический ряд. Для этого все множество возможных значе­ний признака  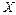разбивается на  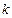непересекающихсяполуоткрытых интервалов

,                                                                   (1.8)

границы которых определяются формулами

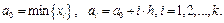                                          (1.9)

Длина каждого интервала h при выбранном числе интервалов, зависящем от объема выборки, равна

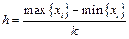.                                                      (1.10)

Оптимальное число интервалов, на которые разбивается диапазон выборки, рекомендуется выбирать по одной из формул (все три формулы дают приблизительно одинаковый результат):

                                                   (1.11)

где [ Q ] – целая часть числа Q.

Эмпирическую частоту попадания  элементов выборки в интервал  обозначим 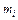. При этом выполняется равенство

.                                                                    (1.12)

Все выборочные значения, попавшие в интервал 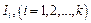принимаются равным его середине  

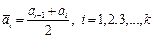,                                               (1.13)

а статистические оценки вероятностей (частота), с которыми выборочная случайная величина X принимает значения равны

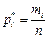,                                                           (1.14)

где 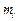  – число выборочных значений (наблюдений), попавших в интервал .

Построение эмпирической функции и плотности распределения

Эмпирической функции распределения  определяют по формуле

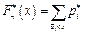,                                                        (1.15)

которую удобно записать в аналитическом виде через накопленные частоты

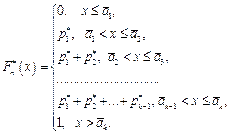                                        (1.16)

Функция представляет собой кусочно-постоянную функцию со скачками в середине интервалов (рис. 1.4).

Рис. 1.4. Пример эмпирической функции распределения при четырех интервалах статистического ряда

 

Эмпирическая плотность распределения вычисляется по формуле

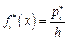.                                                        (1.17)

Аналитическое выражение для эмпирической плотности распределения на каждом интервале можно записать в виде

                                                   (1.18) 

 

График эмпирической плотности распределения строится в виде кусочно-постоянной над интервалами линии и называется гистограммой (рис. 1.5).

Соединив точки гистограммы с абсциссами  при 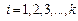 можно построить полигон частот.

Рис. 1.5. Пример гистограммы и полигона частот интервального ряда.

 

Получение точечных и интервальных статистических оценок

Точечными оценками параметров называют такие оценки, которые выражаются каким-то одним числом (точкой).

Таким числом могут быть, например, параметры 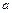 и 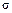 нормального распределения или параметр  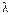закона Пуассона. Не все переменные могут быть оценками.

Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, самостоятельности и эффективности.

1. Несмещенность. Оценка не должна содержать систематической ошибки. Это означает, что математическое ожидание оценки некоторого параметра, взятое по всем возможным выборкам, должно быть равно действительно­му значению параметра.

Если действительное значение оцениваемого параметра обозначить 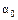, а его оценку , то требование несмещенно­сти запишется в виде .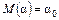

2. Состоятельность. Оценка   должна приближаться к 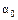 по мере увеличения объема выборки. Но ввиду того, что оценка  является случайной величиной, об этом приближе­нии можно говорить только в вероятностном смысле.

Для состоятельности оценки , получаемой при выборке объема 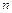,должно выполняться условие сходимости по ве­роятности  к 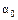, т.е. .

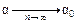 Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются!).

3. Эффективность. Несмещенная оценка  параметра 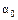 называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок 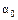, то есть оценка эффективна, если ее дисперсия минимальна.

Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям, и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами.

Если случайная выборка достаточно хорошо воспроизводит распределение исследуемого признака генеральной совокупности, то она называется представительной (ре­презентативной). Поскольку исследуемые элементы генеральной совокуп­ности попадают в выборку случайным образом, случайным будет и значение параметра, определенное с помощью этой выборки. Поэтому по выборке нельзя точно судить о зна­чениях параметров генеральной совокупности. Численные значения параметров генеральной совокупности, получен­ные при изучении выборки, называются их оценками. Различают два вида оценок: точечную и интерваль­ную.