Проверка статистических гипотез

 

Статистическая гипотеза – это предположение отно­сительно вида закона распределения или параметров рас­пределения в генеральной совокупности некоторого при­знака ,являющегося случайной величиной.

По своему содержанию статистические гипотезы можно подразделить на несколько основных типов.

1. Гипотезы о виде закона распределения исследуемой случайной величины.

2. О числовых значениях параметров случай­ной величины.

3. Об общем виде модели, описывающей стати­стическую зависимость между признаками.

4. О принадлежности некоторого признака к тому или иному классу величин.

Естественно, как любая гипотеза, статистическая гипоте­за нуждается в проверке. Проверяемая гипотеза называется основнойилинулевойи обозначается .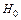

Гипотеза 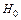 является основной в том смысле, что было бы желательно убедиться в ее справедливости (например,  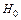– благополучная посадка самолета, выздоровление боль­ного, успех в коммерческой деятельности и т.д.).

Если кроме нулевой выдвигаются и другие гипотезы, то они называются конкурирующимии обозначаются 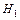,   и т.д.

Правило, по которому принимается решение принять или отклонить 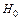, называется статистическим критери­ем.Проверка статистической гипотезы проводится пу­тем рассмотрения некоторого параметра, определяемого по результатам изучения выборки. Этот параметр называется статистикой критерия.

Пусть по некоторым данным имеются основания вы­двинуть предположения о законе распределения или о па­раметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов кото­рой определена эта случайная величина). Задача заключа­ется в том, чтобы подтвердить или опровергнуть это пред­положение, используя выборочные (экспериментальные) данные.

В качестве примера проверки гипотезы о законе распределения генеральной рассмотрим два ста­тистических критерия:  Пирсона и критерий Колмогорова.

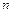Критерий . Сумма квадратов   независимых одинаково распреде­ленных случайных величин подчиняется закону, получив­шему название распределения (1.1).

В качестве статистики критерия Пирсон предложил рас­сматривать величину

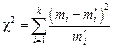.                                                       (1.40)

где 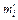- теоретическую частотупопадания элементов выбор­ки в интервал  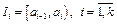 , 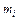- эмпирическая частота попадания элементов выборки в тот же интервал.

Теоретическая частотапопадания элементов выбор­ки в интервал   определяется для каждой области по формуле

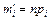,                                                                      (1.41)

где 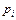 – вероятность попадания признака  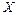в соответст­вии с предполагаемым законом распределения в интервал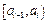

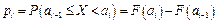,                                  (1.42)

здесь  - границы интервалов статистического ряда, F (x) – гипотетическая функция распределения.

В частности, если основная гипотеза H ₀ состоит в том, что случайная величина X распределена по нормальному закону, то

,                                        (1.43)

где 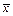- среднее выборочное, 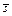- исправленное выборочное среднее квадратическое отклонение, 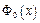- функция Лапласа, которая определяется формулой

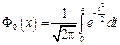
В случае если гипотеза H ₀ состоит в том, что случайная величина X распределена по показательному закону

,                                                    (1.44)

где параметр , 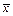- среднее выборочное.

В предположение о равномерном распределении случайной величины X на отрезке 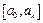, вероятности  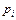определяются по формуле

                                    (1.45)

Число независимых слагаемых, входящих в сумму квадра­тов, называется числом степеней свободыи обозначается .

Так как сумма квадратов – величина всегда неотри­цательная, то кривая распределения лежит в области от нуля до  (рис. 1.4). При  плотность распределения изображается скошенной кривой с максимумом в точке

.

Заметим, что вероятность превышения какого-либо зна­чения  равна площади под кривой распределения от этого значения до . Поэтому за критическоезначение стати­стики принимается значение, площадь под кривой после которого равна уровню значимости 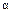. На рис. 1.5 критическая область критерия заштрихована. Значения  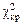в зависимости от  и 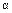 представлены в приложении.

 

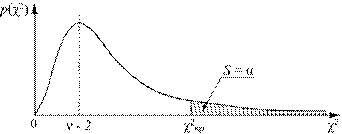
Рис. 1.5. Кривая распределения Пирсона

 

Используя рассчитанные по результатам изучения вы­борки оценки параметров предполагаемого распределения, вводят дополнительные ограничения. Поэтому число степе­ней свободы 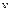 должно быть уменьшено по сравнению с чис­лом слагаемых 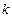,и определяется выражением

,

где 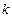 – число рассматриваемых интервалов;  – число пара­метров в принятом распределении; 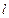 – число независимых линейных ограничивающих связей.

В рассматриваемом случае  из-за одной имеющейся связи: равенство суммы частот объему выборки.

При проверке гипотезы о нормальном распределении признака 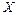  сзаранее неизвестными параметрами  и 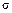 ве­личина  равна 2. Тогда выражение для  при исследовании нормально распределенной величины имеет вид

.

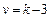По значениям  и 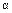 находят значение  по таблицам (прил. 2). Если 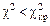, то гипотеза  принимается, а если 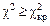, то эта гипотеза отклоняется.

Замечание. Критерий  Пирсона следует применять, если каждая частота  в рассматриваемой области имеет значение не менее 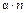. В противном случае нужно укруп­нять области разбиения исследуемого признака.

 

Критерий Колмогорова. Согласно критерию Колмогорова вычисляется статистика

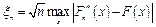                                           (1.46)

в граничных точках интервального ряда, т.е. в точках . Здесь в качестве количественной меры рассматривается максимальное значение абсолютной величины разности между эмпирической функцией распределения  и соответствующей теоретической функцией распределения 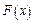(рис. 1.6). При вычислении статистики значения эмпирической функции распределения  определяют по формуле (1.16)

Рис. 1.6. Эмпиричесая функция распределения в в граничных точках интервального ряда и гипотетическая функция .

 

Значения гипотетической функции распределения 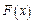  в точке вычисляются в зависимости от выдвинутой гипотезы :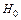

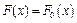
– если выдвинута гипотеза о нормальном распределении, то

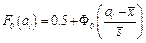,                                            (1.47)

где 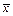- среднее выборочное, 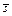- исправленное выборочное среднее квадратическое отклонение, 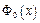- функция Лапласа, значения которой берутся из таблицы;

– если выдвинута гипотеза о показательном распределении, то

,                                             (1.48)

где параметр , 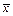- среднее выборочное;

– если выдвинута гипотеза о равномерном распределении, то

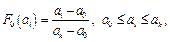                                       (1.49)

где   – границы интервалов интервального ряда.

Выбирая наибольшее значение вычисляется статистика 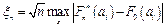. По заданному значению уровня значимости q определяется 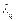такое, что из таблицы распределения Колмогорова. Если 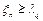, то основная гипотеза отвергается. Если 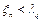, то гипотеза принимается, т.е. генеральное распределение считается совпадающим с гипотетическим. Если 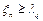, то основная гипотеза отвергается. Если , то гипотеза принимается, т.е. генеральное распределение считается совпадающим с гипотетическим.

 

Общие замечания по критериям согласия. Достоинствами критерия Колмогорова по сравнению с критерием являются возможность его применения при очень маленьких объемах выборки (n < 20), более высокая "чувствительность", а следовательно, меньшая трудоемкость вычислений. Недостатком является то, что эмпирическая функция распределения 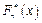 должна быть построена по несгруппированным выборочным данным, что затруднительно при больших объемах выборки. Кроме этого, следует отметить, что критерий Колмогорова можно применять только в случае, когда гипотетическое распределение полностью известно заранее из каких-либо теоретических соображений, т.е. когда известен не только вид функции распределения 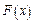, но и все входящие в нее параметры. Такой случай сравнительно редко встречается на практике. Обычно из теоретических соображений известен только общий вид функции , а входящие в нее числовые параметры определяются по данному статистическому материалу. При применении критерия   это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения . Критерий. Колмогорова такого согласования не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения определяются по статистическим данным, критерий дает заведомо заниженные значения ; поэтому мы в ряде случаев рискуем принять как правдоподобную гипотезу, которая в действительности плохо согласуется с опытными данными.

 

1.2. ЗАДАНИЯ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ №3.
ОЦЕНКА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК
СЛУЧАЙНЫХ ДАННЫХ

 

По статистическим данным, полученным в результате проведения опыта, требуется:

1. Произвести группировку, построить статистическое распределение относительных частот и изобразить его графически.

2. Найти эмпирическую функцию распределения и построить ее график.

3. Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, моду, медиану.

4. С надежностью 0,99 найти доверительный интервал для истинного значения рассматириваемой величины.

5. Построить теоретическую нормальную кривую.

6. Выдвинуть гипотезу о законе генерального распределения  и пользуясь критериями  и Колмогорова на уровне значимости 0,01, установить случайно или значимо расхождение между формой распределения выборки и генеральной совокупности.