Интервальные оценки параметров случайной величины

Пусть по результатам опыта построена точечная оцен­ка  параметра . Точечная оценка  параметра  дает лишь некоторое приближенное значение .

Возникает вопрос: насколько эта оценка точна и достовер­на? Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.

Интервальная оценка параметра  (  или ) при­знака 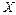  генеральной совокупности имеет следующий вид:

 или ,

где  – наибольшее отклонение выборочного значения па­раметра от его истинного значения, или предельная ошиб­ка выборки(точность оценки, отклонение).

Очевидно, что это неравенство, определяющее попадание  в ука­занный интервал, при заданной точности оценки  верно лишь с какой-то вероятностью , которая называется дове­рительной вероятностью.

На практике обычно заранее задают доверительную вероятность , причем наиболее час­то берут значения ;  и .

Интервал  называется доверительным интервалом.В качестве  берут точечную несмещенную оценку , полученную по результатам выборки. Следова­тельно, задача состоит в том, чтобы по заданной величине  найти Δ.

Чтобы получить интервальную оценку генеральной сред­ней , нужно найти такую величину Δ, для которой

  .                                           (1.34)

Пусть известна генеральная дисперсия  признака . Так как неравенство   эквивалентно неравенству , а неравенство   эквивалентно неравенст­ву , то выражение (1.29) эквивалентно выражению

.

Здесь 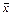 – случайная величина, и если признак   рас­пределен нормально, то 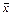  тоже распределена нормально. Так как  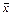– несмещенная оценка , то .

Можно доказать, что если дисперсия признака   рав­на , то дисперсия случайной величины 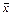, являющей­ся средним арифметическим  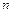 одинаково распределенных случайных величин с дисперсией , равна , а среднее квадратическое отклонение случайной величины 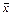, следовательно, равно .

Тогда можно также показать, что

,                                        (1.35)

где  – функция Лапласа (прил. 1).

Отсюда следует, что для нахождения  нужно решить уравнение .

Уравнение решается так. Обозначим  и найдем по таблице значений функции Лапласа  (прил. 1) такое , что .

Вычислим окончательно  по следующей формуле

.                                                            (1.36)

Следовательно, доверительный интервал   для довери­тельной вероятности  имеет вид

.                                                (1.37)

Такую оценку используют, когда объем выборки .

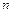Если генеральная дисперсия  неизвестна, то она час­то заменятся ее несмещенной оценкой , хотя при небольших   это ведет к существенному уменьшению доверительного интервала.

Доверительный интервал получается точнее, если при этом вместо   взять параметр   распределения Стьюдента, который можно найти в прил. 3 по из­вестным значениям  и .

Тогда доверительный интервал для генеральной средней при неизвестной генеральной дисперсии имеет вид

.                                                  (1.38)

Интервальной оценкой (с надёжностью ) среднего квадратического отклонения 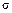 нормально распределенного количественного признака  «по исправленному» выборочному среднему квадратическому отклонению  служит доверительный интервал

                                          (1.39)

где  находят из таблицы (прил. 4) по заданным 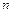 и .