Точечные оценки параметров случайной величины

 

Поскольку точные значения параметров распределения признака 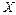  в генеральной совокупности в боль­шинстве случаев определить не представляется возмож­ным, то эти параметры следует оценить, используя соответ­ствующие параметры выборки.

Числовые характеристики выборки называются выборочными (эмпирическим) характеристиками.

Основные числовые характеристики:

- среднее арифметическое (выборочное среднее)

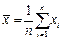;                                                         (1.19а)

при дискретной группировке

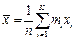;                                                        (1.19б)

при интервальной группировке

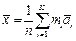,                                                         (1.19в)

где 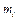- частота, K - количество интервалов, 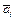- середина i -го интервала.

- выборочная (эмпирическая) дисперсия

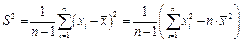                             (1.20а)

при дискретной группировке

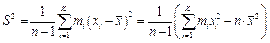;                      (1.20б)

при интервальной группировке

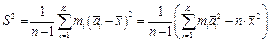.                      (1.20в) 

- выборочные начальные и центральные моменты порядка l

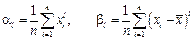                                           (1.21а)

при дискретной группировке

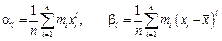;                                   (1.21б)

при интервальной группировке

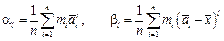.                                   (1.21в)

- коэффициент вариации

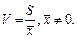                                                       (1.22)

- оценка коэффициента асимметрии A (характеризует симметричность распределения относительно среднего )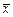

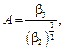                                                           (1.23)

при интервальной группировке

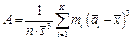                                           (1.24)

- оценка эксцесса E (меры островершинности распределения по сравнению с нормальным распределением)

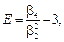                                                          (1.25)

при интервальной группировке

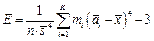.                                   (1.26)

Если 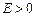, то вершина более острая, а если 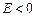, то более плоская, чем у нормального распределения. У нормального распределения .

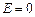- выборочная мода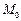

При дискретной группировке (вариационный ряд) мода определяется как значение варианты с наибольшей частотой.

При интервальной группировке выбирается интервал, которому соответствует наибольшая частота. Пусть это k -й интервал 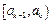, его частота равна 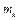, а ширина h, тогда

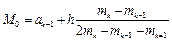.                                    (1.27)

- выборочная медиана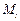

Если выборка объема n представлена вариационным рядом, то

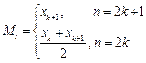                                                       1.28)

При интервальной группировке сначала находят так называемый медианный интервал 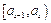, номер s которого определяется из неравенств

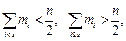                                           (1.29)

где 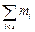- сумма частот всех интервалов левее медианного, 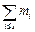- сумма частот, включающая частоту медианного интервала.

Медиану оценивают с помощью следующей интерполяционной формулы

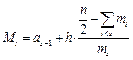,                                                      (1.30)

где 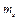 - частота медианного интервала.

Таким образом, в качестве точечной оценки параметров распределения признака 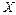  в генеральной совокупности может приниматься соответствующие пара­метры выборки. Например, для параметров генеральной совокупност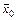и  и 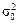 (нормальное распределение) можно доказать следующее.

1. 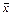 является несмещенной точечной оценкой 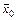, т.е.

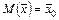.                                                              (1.31)

2. Оценка 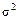 для генеральной дисперсии  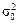является состоятельной, но несмещенной. Поэтому вводят величину

,

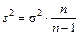которая называется исправленной статистической выборочной дисперсией. Эта величина является несмещенной оценкой генеральной дисперсии 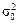, т.е.

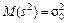.                                                            (1.32)

Величина 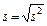называется исправленным выборочным средним квадратическим отклонением и является несмещенной точечной оценкой генерального среднего квадратического отклонения 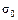, т.е.

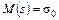.                                                                 (1.33)