Проиллюстрируем идею метода на простейшем примере:
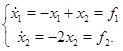
Рассмотрим функцию 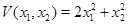 . Эта функция положительна всюду, кроме точки
. Эта функция положительна всюду, кроме точки 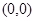 , где она обращается в нуль. В пространстве переменных
, где она обращается в нуль. В пространстве переменных  уравнение
уравнение 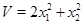 определяет параболоид с вершиной в начале координат. Линии уровня этой поверхности на плоскости
определяет параболоид с вершиной в начале координат. Линии уровня этой поверхности на плоскости 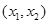 представляют собой эллипсы. Зададим произвольно малое
представляют собой эллипсы. Зададим произвольно малое 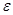 . Построим на плоскости
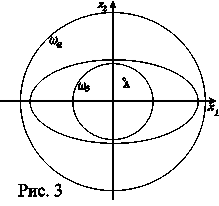
. Построим на плоскости 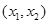 круг
круг 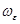 радиуса
радиуса 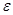 . Возьмем одну из линий уровня --- эллипс, целиком лежащий внутри круга
. Возьмем одну из линий уровня --- эллипс, целиком лежащий внутри круга 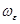 . Построим другой круг
. Построим другой круг 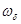 целиком лежащий внутри эллипса (рис. 3).
целиком лежащий внутри эллипса (рис. 3).
Пусть начальная точка 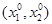 лежит внутри
лежит внутри 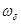 .
.
Рассмотрим функцию двух переменных 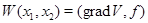 . Легко видеть, что если вместо
. Легко видеть, что если вместо 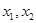 подставить решение системы, то полученная таким образом, функция от
подставить решение системы, то полученная таким образом, функция от 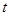 будет представлять собой полную производную функции
будет представлять собой полную производную функции 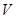 вдоль траектории решения системы. Если эта производная вдоль любой траектории, начинающейся в
вдоль траектории решения системы. Если эта производная вдоль любой траектории, начинающейся в 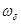 , неположительна, то это будет означать, что траектория не сможет покинуть
, неположительна, то это будет означать, что траектория не сможет покинуть 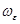 , так как иначе между
, так как иначе между 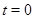 и значением
и значением 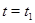 , при котором она попадет на границу
, при котором она попадет на границу 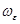 , найдется значение
, найдется значение 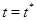 , для которого
, для которого 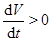 , поскольку
, поскольку 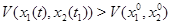 . То, что ни одна траектория, начинающаяся в
. То, что ни одна траектория, начинающаяся в  , не покидает ни при одном
, не покидает ни при одном 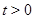 круг
круг 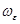 , означает устойчивость тривиального решения.
, означает устойчивость тривиального решения.
Итак, мы должны проверить знак 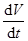 вдоль траектории. Для этого надо знать саму траекторию. Хотя в данном примере это можно сделать, но метод должен быть рассчитан на систему общего вида, для которого
вдоль траектории. Для этого надо знать саму траекторию. Хотя в данном примере это можно сделать, но метод должен быть рассчитан на систему общего вида, для которого 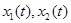 нельзя выписать явно и тем самым нельзя проверить нужное неравенство. Поэтому мы будем требовать, чтобы функция
нельзя выписать явно и тем самым нельзя проверить нужное неравенство. Поэтому мы будем требовать, чтобы функция 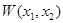 была неположительной как функция двух независимых переменных
была неположительной как функция двух независимых переменных  по крайней мере в некоторой окрестности
по крайней мере в некоторой окрестности  . Это условие можно проверить непосредственно по правым частям системы не зная решения. В нашем примере именно так и будет, поскольку
. Это условие можно проверить непосредственно по правым частям системы не зная решения. В нашем примере именно так и будет, поскольку 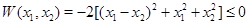 всюду на плоскости
всюду на плоскости 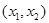 , а тем самым вдоль любой траектории, и устойчивость тривиального решения гарантирована. Функция
, а тем самым вдоль любой траектории, и устойчивость тривиального решения гарантирована. Функция 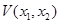 и есть функция Ляпунова для рассмотренного примера. Она имеет вид квадратичной формы, хотя в принципе можно было взять любую другую функцию, лишь бы она была положительной всюду, кроме точки
и есть функция Ляпунова для рассмотренного примера. Она имеет вид квадратичной формы, хотя в принципе можно было взять любую другую функцию, лишь бы она была положительной всюду, кроме точки  , где она обращается в нуль, а выражение
, где она обращается в нуль, а выражение 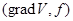 было неположительное. Обратимся теперь к формулировке некоторых общих теорем, в основу которых положена эта идея. Будем исследовать тривиальное решение системы.
было неположительное. Обратимся теперь к формулировке некоторых общих теорем, в основу которых положена эта идея. Будем исследовать тривиальное решение системы.
Все дальнейшие построения будем вести в некоторой 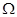 -окрестности начала координат в фазовом пространстве. Пусть для определенности
-окрестности начала координат в фазовом пространстве. Пусть для определенности 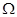 задается неравенством
задается неравенством 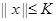 ,
, 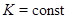 . Функция
. Функция 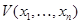 (или короче
(или короче 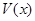 ) называется положительно определенной в
) называется положительно определенной в 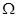 , если
, если 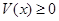 в
в 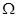 , причем
, причем 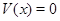 тогда и только тогда, когда
тогда и только тогда, когда 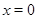 .
.
Приведем ряд утверждений, показывающих применение функций Ляпунова.
 2020-05-21
2020-05-21 153
153








