2020-05-21
151
Рассмотрим систему дифференциальных уравнений
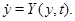
Выделим некоторое решение 
системы и назовем его невозмущенным решением.
Решение назовем устойчивым в смысле Ляпунова, если для любого 
можно указать 
такое, что из неравенства 
следует неравенство 
при 
. Здесь через 
обозначено любое другое решение системы, определяемое начальным условием 
. Решение 
называется асимптотически устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и если существует такое 
, что при 
будем иметь
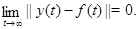
Пример Решение 
уравнения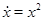 
не является устойчивым ни справа, ни слева, т.к. каждое решение 
, где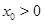 
(
), перестает существовать при 
(рис. 1).
Пример. Решение 
уравнения 
неустойчиво справа, т.к. все решения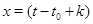 
, 
, 
, приближаются к 
при 
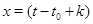. Каждое решение так же, как и решение 
, является асимптотически устойчивым справа (рис. 2).
Проведем в системе замену переменных 
. Новая система будет иметь вид
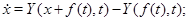
вводя обозначение
получим систему
где 
при 
. Решение перешло при рассматриваемой замене переменных в положение равновесия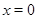 
новой системы. Задача устойчивости решения переходит, таким образом, в задачу устойчивости нулевого (тривиального) решения 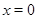системы.
Приведем определение устойчивости нулевого решения системы.
Решение 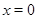системы называется устойчивым в смысле Ляпунова, если для любого 
можно указать 
такое, что из неравенства 
следует неравенство 
при . Если же, кроме того, всякое решение 
, начальные данные которого определяются условием 
, обладает свойством 
, то нулевое решение называется асимптотически устойчивым в смысле Ляпунова.
