Необходимый признак сходимости ряда

ВЫСШАЯ МАТЕМАТИКА

КОНСПЕКТЫ ЛЕКЦИЙ

№ 9-10 (25-26)

Содержание
§ 1.	Основные понятия…………………………………….…………………………...	3
§ 2.	Необходимый признак сходимости ряда……..………………………………...	5
§ 3.	Свойства сходящихся рядов…………………………………………………..	5
§ 4.	Положительные ряды ……………..…………………………………………	7
§ 5.	Первый признак сравнения……..………………………………………………...	8
§ 6.	Второй признак сравнения……..………………………………………………...	8
§ 7.	Признак Даламбера……..………………………………………………..................	9
§ 8.	Радикальный признак Коши……..………………………………………………..	9
§ 9.	Интегральный признак Коши…..…………………………………………………	10
§ 10.	Знакочередующиеся ряды. Признак Лейбница……………………………...	11
§ 11.	Знакопеременные ряды. Абсолютно и условно сходящиеся ряды………...	12

 

 

 

Лекция 9-10 (25-26)

 

Основные понятия. Необходимый признак сходимости ряда. Свойства сходящихся рядов. Положительные ряды. Первый признак сравнения. Второй признак сравнения. Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. Знакочередующиеся ряды. Признак Лейбница. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды.

 

 

 

Основные понятия

 

Пусть 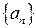 – произвольная последовательность вещественных или комплексных чисел. Бесконечная сумма

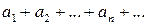   или

называется числовым рядом. Каждое из чисел последовательности 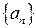 называется членом числового ряда, причем

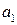 – первым членом,

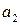 – вторым членом,

 ………………………………….

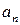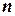 – -м или общим членом числового ряда.

Так как пока рассматриваются только числовые ряды, поэтому числовой ряд будем коротко писать одним словом ряд.

Ряд считается заданным, если задан его общий член 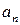. Например, если общим членом ряда является 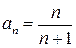, то ряд имеет вид

.

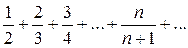Сложной, а точнее некорректной является обратная задача, то есть по нескольким первым членам найти общий член ряда. Некорректность заключается в том, что эта задача имеет бесчисленно много решений. Однако, как правило, можно найти самый простой и естественный ответ. Например, если первыми членами ряда являются числа, 1, 2, 3, то самым простым и естественным ответом для общего члена является ответ: . Заметим, что для произвольной последовательности 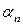, первыми тремя значениями последовательности  также являются числа 1, 2 и 3. Так как мы условились среди всех ответов брать самый простой и естественный, то остановимся на вариант .

Пусть задан ряд . По этому ряду составим числовую последовательность :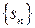

,

,

,

……………………

,

……………………

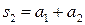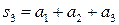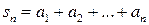Построенная последовательность называется последовательностью частичных сумм, а  – 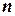-й частичной суммой ряда. Если из данного ряда отбросить 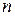-ю частичную сумму, то оставшаяся часть называется 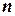-мостатком ряда и обозначается 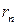, то есть .

Числовой ряд  называется сходящимся, если последовательность частичных сумм 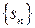 имеет конечный предел. Если существует конечный предел 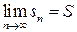, то число  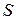называется суммой ряда и можно писать

или .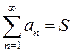

Если последовательность частичных сумм 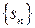 не имеет конечный предел.(предел бесконечный или не существует), то ряд называется расходящимся.

Предостережение 1.1. Перестановка слагаемых в конечной сумме не влияет на ее результат («От перемены мест слагаемых сумма не меняется»). Если же сумма состоит из бесконечного числа слагаемых, то перестановка слагаемых может влиять на ее результат. Справедливость этого предостережения будет следовать из теоремы Римана.

Предостережение 1.2. Раскрытие скобок в конечной сумме не влияет на ее результат. Если же сумма состоит из бесконечного числа слагаемых, то раскрытие скобок может влиять на ее результат. Например, ряд

является сходящимся. Если раскрыть скобки, то получится расходящийся ряд:

.

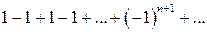Предостережение 1.3. Ввод скобок в конечной сумме не влияет на ее результат. Если же сумма состоит из бесконечного числа слагаемых, то ввод скобок может влиять на ее результат. Например, ряд

.

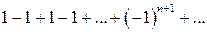Ряды

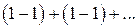и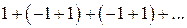

получаются вводом скобок из данного ряда. Эти ряды являются сходящимися: сумма первого равна 0, а второго равна 1.

 

Необходимый признак сходимости ряда

 

Отметим одно важное свойство, присущее всем сходящимся рядам.

Теорема 2.1. (Необходимый признак сходимости ряда). Если ряд   является сходящимся, то предел его общего члена 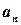  равен нулю:

 – сходится Þ .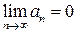

Замечание. Данная теорема выражает лишь необходимый признак сходимости ряда. Этот необходимый признак не является достаточным, то есть из выполнения условия 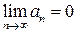 еще не следует сходимость ряда .

Предостережение 2.1. Всякое утверждение о сходимости ряда, которое делается, ссылаясь на теорему необходимости, является неверным.