2020-05-21
88
Теорема 9.1. Пусть ряд 
является положительным, члены которого образуют монотонно убывающую (не возрастающую) последовательность
,
а функция 
определена на промежутке 
, и на этом промежутке непрерывна, монотонно убывающая (не возрастающая) и
.
Тогда:
1) из сходимости несобственного интеграла 
вытекает сходимость данного ряда;
2) из расходимости несобственного интеграла вытекает расходимость данного ряда.
Замечание. Если в записи ряда номер 
начинается не с 
, а с некоторого номера 
, то и функция 
должна удовлетворять условии теоремы 9.1 на промежутке 
, и следует рассматривать несобственный интеграл на этом промежутке: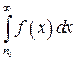 
.
В качестве примера рассмотрим обобщенный гармонический ряд 
.
Положим 
. Эта функция определена, непрерывна и монотонно убывает на промежутке 
, то есть удовлетворяет всем условиям
теоремы 9.1. Поэтому сходимость данного ряда равносильна сходимости несобственного интеграла 
. Имеем
.
Если 
, то
;
если 
, то 
, и, следовательно,
;
если 
, то 
, и, следовательно,
|
|
|
.
Таким образом, имеем
Итак, обобщенный гармонический ряд сходится при 
и расходится при 
.
Знакочередующиеся ряды. Признак Лейбница
Ряд называется знакочередующимся, если за каждым положительным членом следует отрицательный, а за каждым отрицательным – положительный:
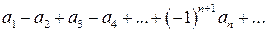
или
,
где
.
Теорема 10.1. (Признак Лейбница) Пусть:
1) предел общего члена знакочередующегося ряда равен нулю,
то есть 
;
2) абсолютные величины его членов монотонно убывают (не возрастают), то есть 
.
