Свойства сходящихся рядов

Пусть – данный ряд, а – произвольное число. Произведением ряда на число , называется ряд .

Теорема 3.1. Пусть ряд является сходящимся, а – произвольное число. Тогда ряд является сходящимся рядом и справедливо равенство:

.

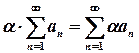Смысл этой теоремы заключается в том, что если ряд является сходящимся, то постоянный множитель можно вынести за знак суммы, или, что то же самое, постоянный множитель можно вынести за скобки, и в случае бесконечного числа слагаемых.

Эту теорему можно обращать: если ряд хотя бы при одном ненулевом значении является сходящимся, то и ряд является сходящимся.

Пусть и – данные ряды. Ряд называется суммой рядов и , а ряд – их разностью.

Теорема 3.2. Сумма сходящихся рядов и является сходящимся рядом и справедливо равенство

.

Смысл этой теоремы заключается в том, что в бесконечной сумме

можно раскрывать скобки (сравните с Предостережением 2), перегруппировать слагаемые (сравните с Предостережением 1), вводить скобки (сравните с Предостережением 3) и представить бесконечную сумму в виде

.

Как следствие из теорем 1 и 2 получим следующую теорему.

Теорема 3.3. Разность сходящихся рядов и является сходящимся рядом и справедливо равенство

.

Замечание. Если ряд сходится, а ряд расходится, то для любых и ряд расходится.

Теорема 3.4. 1) Если ряд сходится, то сходится и любой его остаток 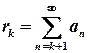; 2) если какой-либо остаток ряда сходится, то сходится и сам ряд, при этом справедливо равенство

,

где

.

Из теоремы 3.4 следует:

1) ;

2) отбрасывание или добавление конечного числа членов к данному ряду не влияет на его сходимость.

Положительные ряды

Ряд называется положительным, если все члены этого ряда являются положительными числами.

Последовательность частичных сумм любого положительного ряда является строго монотонно возрастающей последовательностью:

Теорема 4.1. (Достаточное условие сходимости положительных рядов). Для сходимости положительного ряда, необходимо и достаточно ограниченность его последовательности частичных сумм.

Это свойство характерно только для положительных рядов. В общем случае, даже ограниченность последовательности частичных сумм, не является достаточным, для сходимости ряда.

Отсюда вытекает признак расходимости положительных рядов: для расходимости положительного ряда, необходимо и достаточно неограниченность сверху последовательности частичных сумм, то есть выполнение равенства .

Отметим еще одно важное свойство положительных рядов. Если некоторая подпоследовательность последовательности частичных сумм положительного ряда сходится (не сходится), то и сама последовательность частичных сумм сходится (не сходится).